题目内容
12.P是椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1上的一点,A、B分别是圆(x+3)2+y2=1和(x-3)2+y2=1上的点,则|$\overrightarrow{PA}$|+|$\overrightarrow{PB}$|的取值范围是[8,12].分析 由题设知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的左右焦点分别是两圆(x+3)2+y2=1和(x-3)2+y2=1的圆心,由此能求出|$\overrightarrow{PA}$|+|$\overrightarrow{PB}$|的最小值、最大值.
解答 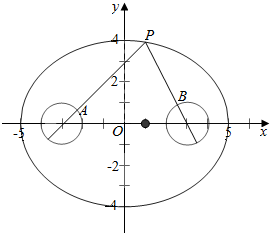 解:依题意,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的焦点分别是
解:依题意,椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1的焦点分别是
两圆(x+3)2+y2=1和(x-3)2+y2=1的圆心,
所以(|$\overrightarrow{PA}$|+|$\overrightarrow{PB}$|)max=2×5+2=12,
(|$\overrightarrow{PA}$|+|$\overrightarrow{PB}$|)min=2×5-2=8,
则|$\overrightarrow{PA}$|+|$\overrightarrow{PB}$|的取值范围是[8,12].
故答案为:[8,12].
点评 本题考查圆锥曲线的性质和应用,解题时要认真审题,仔细解答,注意公式的合理运用

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.一个命题p的逆命题是一个假命题,则下列判断一定正确的是( )
| A. | 命题p是真命题 | B. | 命题p的否命题是假命题 | ||
| C. | 命题p的逆否命题是假命题 | D. | 命题p的否命题是真命题 |
3.在长方体ABCD-A1B1C1D1的棱AB,AD,AA1,上分别各取异于端点的一点E,F,M,则△MEF是( )
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 不能确定 |
17.在(x2+x-2)4的展开式中,各项系数的和是( )
| A. | 0 | B. | 1 | C. | 16 | D. | 256 |
4.已知△ABC,P为三角形所在平面上的一点,且点P满足:a$•\overrightarrow{PA}$+b$•\overrightarrow{PB}$+c$•\overrightarrow{PC}$=0,则P点为三角形( )
| A. | 外心 | B. | 内心 | C. | 重心 | D. | 垂心 |
2.已知正数x、y满足x+y=xy,则4x,y,$\frac{1}{x}$,$\frac{1}{y}$这4个数的平均数的( )
| A. | 最小值为2 | B. | 最小值为$\frac{5}{2}$ | C. | 最大值为2 | D. | 最大值为$\frac{5}{2}$ |
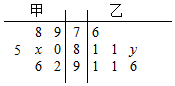 高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.
高三年级从甲(文)、乙(理)两个科组各选出7名学生参加高校自主招生数学选拔考试,他们取得的成绩的茎叶图如图所示,其中甲组学生的平均分是85,乙组学生成绩的中位数是83.