题目内容
1.已知x,y都是锐角,且tanx=3tany,证明:x-y≤$\frac{π}{6}$.分析 先用两角差的正切公式,求一下tan(x-y)的值,然后再由已知代换,利用均值不等式求得tan(x-y)的最大值,从而得到结果.
解答 证明:因为x,y都是锐角,x-y∈(0,$\frac{π}{2}$),且tanx=3tany,
所以tan(x-y)=$\frac{tanx-tany}{1+tanxtany}$=$\frac{2tany}{1+3ta{n}^{2}y}$
=$\frac{2}{\frac{1}{tany}+3tany}$≤$\frac{2}{2\sqrt{\frac{1}{tany}•3tany}}$=$\frac{\sqrt{3}}{3}$=tan$\frac{π}{6}$,当且仅当3tan2y=1时取等号,
∴x-y≤$\frac{π}{6}$.
点评 本题是中档题,考查两角和与差的正切函数的应用,基本不等式的应用,注意角的范围,考查计算能力.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
9.乘积(x+y+z)(a-b+c)(m-n+p+q-3)展开后共有( )项.
| A. | 11 | B. | 12 | C. | 45 | D. | 120 |
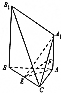 如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.
如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.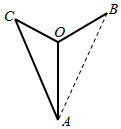 如图是某设计师设计的Y型饰品的平面图,其中支架OA,OB,OC两两成120°,OC=1,AB=OB+OC,且OA>OB,现设计师在支架OB上装点普通珠宝,普通珠宝的价值为M,且M与OB长成正比,比例系数为k(k为正常数):在△AOC区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为N,且N与△AOC的面积成正比,比例系数为4$\sqrt{3}$k,设OA=x,OB=y.
如图是某设计师设计的Y型饰品的平面图,其中支架OA,OB,OC两两成120°,OC=1,AB=OB+OC,且OA>OB,现设计师在支架OB上装点普通珠宝,普通珠宝的价值为M,且M与OB长成正比,比例系数为k(k为正常数):在△AOC区域(阴影区域)内镶嵌名贵珠宝,名贵珠宝的价值为N,且N与△AOC的面积成正比,比例系数为4$\sqrt{3}$k,设OA=x,OB=y.