题目内容
20.设全集为R,集合M={x∈R|x2-4x+3>0},集合N={x∈R|2x>4},则M∪N=(-∞,1)∪(2,+∞);M∩N=(3,+∞);∁R(M∩N)=(-∞,3].分析 解一元二次不等式化简集合M,解指数不等式化简集合N,则M∪N,M∩N,∁R(M∩N)的答案可求.
解答 解:M={x∈R|x2-4x+3>0}={x∈R|x<1或x>3},N={x∈R|2x>4}={x∈R|x>2},
则M∪N={x∈R|x<1或x>3}∪{x∈R|x>2}=(-∞,1)∪(2,+∞);
M∩N={x∈R|x<1或x>3}∩{x∈R|x>2}=(3,+∞);
∁R(M∩N)=(-∞,3].
故答案为:(-∞,1)∪(2,+∞);(3,+∞);(-∞,3].
点评 本题考查了交、并、补集的混合运算,考查了一元二次不等式和指数不等式的解法,是基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
10.已知定义在R上的奇函数f(x)满足f(x)=2x-4(x>0),则{x|f(x-1)>0}等于( )
| A. | {x|x>3} | B. | {x|-1<x<1} | C. | {x|-1<x<1或x>3} | D. | {x|x<-1} |
9.乘积(x+y+z)(a-b+c)(m-n+p+q-3)展开后共有( )项.
| A. | 11 | B. | 12 | C. | 45 | D. | 120 |
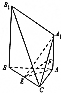 如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.
如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.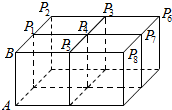 如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )
如图,四个完全相同的长方体排成一个直四棱柱:每个长方体底面为边长1的正方形,侧棱AB长为2,Pi(i=1,2…)是上底面上其余的八个点,则$\overrightarrow{AB}$•$\overrightarrow{A{P}_{i}}$(i=1,2,…)的不同值的个数为( )