题目内容
3.在长方体ABCD-A1B1C1D1的棱AB,AD,AA1,上分别各取异于端点的一点E,F,M,则△MEF是( )| A. | 钝角三角形 | B. | 锐角三角形 | C. | 直角三角形 | D. | 不能确定 |
分析 根据题意,画出图形,结合图形,设出AE=x,AF=y,AM=z,利用勾股定理和余弦定理,求出△MEF的内角的余弦值,即可判断三角形的形状.
解答 解:如图所示,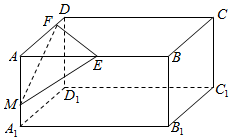
设AE=x,AF=y,AM=z,
则EF2=x2+y2,MF2=y2+z2,ME2=x2+z2,
∴cos∠EMF=$\frac{{ME}^{2}{+MF}^{2}{-EF}^{2}}{2•ME•MF}$=$\frac{{z}^{2}}{\sqrt{{(x}^{2}{+z}^{2}){(y}^{2}{+z}^{2})}}$>0,
∴∠EMF为锐角;
同理,∠EFM、∠FEM也是锐角,
∴△MEF是锐角三角形.
故选:B.
点评 本题考查了利用余弦定理判断三角形形状的应用问题,也可以用平面向量的坐标表示求向量的夹角进行判断,是基础题目.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.下列说法正确的是( )
| A. | 命题“p∨q”为真命题,则命题“p”和命题“q”均为真命题 | |
| B. | 已知x∈R,则“x>1”是“x>2”的充分不必要条件 | |
| C. | 命题“?x∈R,x2-x>0”的否定是:“?x∈R,x2-x≤0” | |
| D. | 命题“若am2<bm2,则a<b”的逆命题是真命题 |
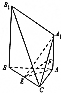 如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.
如图,已知A1A⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.