题目内容

12．曲线y=$\frac{lnx}{{x}^{2}}$在点（1，0）处的切线方程是y=x-1．

分析 求出曲线y=$\frac{lnx}{{x}^{2}}$在点（1，0）处切线的斜率，由此能求出曲线y=$\frac{lnx}{{x}^{2}}$在点（1，0）处的切线方程．

解答 解：∵y=$\frac{lnx}{{x}^{2}}$，∴y′=$\frac{x-2xlnx}{{x}^{4}}$，
∴曲线y=$\frac{lnx}{{x}^{2}}$在点（1，0）处切线的斜率k=1，
曲线y=$\frac{lnx}{{x}^{2}}$在点（1，0）处切线的方程为：y=x-1．
故答案为：y=x-1．

点评 本题考查曲线的切线方程的求法，是基础题．解题时要认真审题，注意导数的几何意义的合理运用．

练习册系列答案
相关题目
2．下列各数中最大的数为（　　）
A．101111（2）B．1210（3）C．112（8）D．69（12）
3．下列函数中，是偶函数且在区间（0，+∞）上单调递减的函数是（　　）
A．y=2xB．y=$\sqrt{x}$C．y=|x|D．y=-x2+1
20．已知向量$\overrightarrow{a}$=（3，-2），$\overrightarrow{b}$=（x，y-1），且$\overrightarrow{a}$∥$\overrightarrow{b}$，若x，y均为正数，则$\frac{3}{x}$+$\frac{2}{y}$的最小值是8．
7．定义平面上一点P到曲线C的距离为点P到曲线C上所有点距离的最小值，那么平面内到定圆的距离与到定点A的距离相等的点的轨迹不可能是（　　）
A．圆B．椭圆C．双曲线的一支D．直线
17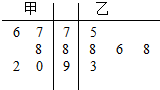．甲、乙两位歌手在“中国好声音”选拔赛中，5次得分情况如茎叶图所示，记甲、乙两人的平均得分分别为x甲、x乙，则下列判断正确的是（　　）
A．x甲＜x乙，甲比乙成绩稳定B．x甲＜x乙，乙比甲成绩稳定
C．x甲＞x乙，甲比乙成绩稳定D．x甲＞x乙，乙比甲成绩稳定
4．下列四个判断：
①某校高三一班和高三二班的人数分别是m，n，某次测试数学平均分分别是a，b，则这两个班的数学的平均分为$\frac{a+b}{2}$；
②10名工人某天生产同一种零件，生产的件数是15，17，14，10，15，17，17，16，14，12，设其平均数为a，中位数为b，众数为c，则有c＞a＞b；
③设从总体中抽取的样本为（x1，y1），（x2，y2），…，（xn，yn），若记$\overline{x}$=$\frac{1}{n}$$\sum_{i=1}^{n}$xi，$\overline{y}$=$\frac{1}{n}$$\underset{\stackrel{n}{\;}}{i=1}$yi，则回归直线方程$\stackrel{∧}{y}$=bx+a必过点（$\overline{x}$，$\overrightarrow{y}$）； 
④已知ξ服从正态分布N（0，σ2），且P（-2≤ξ≤0）=0.4，则P（ξ＞2）=0.2．
其中正确判断的个数有（　　）
A．0个B．1个C．2个D．3个
1．函数$y=sin（\frac{1}{2}x+\frac{π}{4}）$的周期为4π．
2．设a，b是两条不同直线，下列命题α，β，γ是三个不同平面，下列命题不正确的是（　　）
A．b?α，a∥b⇒a∥αB．a∥α，α∩β=b，a?β⇒a∥b
C．a?α，b?α，a∩b=p，a∥β，b∥β⇒α∥βD．α∥β，α∩γ=a，β∩γ=b⇒a∥b

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网