题目内容
20.已知向量$\overrightarrow{a}$=(3,-2),$\overrightarrow{b}$=(x,y-1),且$\overrightarrow{a}$∥$\overrightarrow{b}$,若x,y均为正数,则$\frac{3}{x}$+$\frac{2}{y}$的最小值是8.分析 根据向量$\overrightarrow{a}$∥$\overrightarrow{b}$,得出2x+3y=3,再根据基本不等式求出$\frac{3}{x}$+$\frac{2}{y}$的最小值.
解答 解:∵向量$\overrightarrow{a}$=(3,-2),$\overrightarrow{b}$=(x,y-1),且$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴3(y-1)+2x=0,
即2x+3y=3;
又x,y均为正数,
∴$\frac{3}{x}$+$\frac{2}{y}$=$\frac{2x+3y}{x}$+$\frac{2(2x+3y)}{3y}$=4+$\frac{3y}{x}$+$\frac{4x}{3y}$≥4+2$\sqrt{\frac{3y}{x}•\frac{4x}{3y}}$=8,
当且仅当$\frac{3y}{x}$=$\frac{4x}{3y}$,即2x=3y=$\frac{3}{2}$时取“=”;
∴$\frac{3}{x}$+$\frac{2}{y}$的最小值是8.
故答案为:8.
点评 本题考查了基本不等式的应用问题,也考查了平面向量的共线问题,是基础题目.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
8.执行如图所示的程序框图,若p=0.9,则输出的n为( )


| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
15.2015年十一黄金周期间,渭南日报记者通过随机询问本市华山景区220名游客对景区的服务是否满意情况,得到如下的统计表:(单位:名)
(Ⅰ)从这100名女游客中按对华山景区的服务是否满意采取分层抽样,抽取一个容量为5的样本,问样本中满意与不满意的女游客各有多少名?
(Ⅱ)从(Ⅰ)中的5名女游客样本中随机选取两名作深度访谈,求选出满意与不满意的女游客一名的概率;
(Ⅲ)根据以上统计表,问有多大把握认为“游客性别与对华山景区的服务满意”有关.
附:
K2=$\frac{n(ad-bc)^2}{(a+b)(c+d)(a+c)(b+d)}$.
| 男 | 女 | 总计 | |
| 满意 | 100 | 60 | 160 |
| 不满意 | 20 | 40 | 60 |
| 总计 | 120 | 100 | 220 |
(Ⅱ)从(Ⅰ)中的5名女游客样本中随机选取两名作深度访谈,求选出满意与不满意的女游客一名的概率;
(Ⅲ)根据以上统计表,问有多大把握认为“游客性别与对华山景区的服务满意”有关.
附:
| P(K2≥K0) | 0.050 | 0.025 | 0.010 |
| K0 | 3.841 | 5.024 | 6.635 |
5.下列说法中,正确的是( )
| A. | 垂直于同一直线的两条直线互相平行 | |
| B. | 垂直于同一平面的两条直线互相平行 | |
| C. | 垂直于同一平面的两个平面互相平行 | |
| D. | 平行于同一平面的两条直线互相平行 |
9.下列各角中,与50°的角终边相同的角是( )
| A. | -310° | B. | -50° | C. | 140° | D. | 40° |
10. 一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( )
一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( )
 一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( )
一个几何体的三视图如图所示,正视图为直角三角形、侧视图为等边三角形,俯视图为直角梯形,则该几何体的体积等于( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
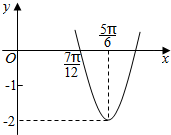 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-1.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)在区间[0,$\frac{π}{2}$]上的最小值为-1.