题目内容
数列1,
,
,…,
,…是( )
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
| A、递增数列 | B、递减数列 |
| C、常数列 | D、摆动数列 |
考点:数列的函数特性
专题:等差数列与等比数列
分析:根据数列项的关系即可得到结论,
解答:
解:∵函数y=
是减函数,
∴数列1,
,
,…,
,…是递减数列,
故选:B.
| 1 |
| 2x-1 |
∴数列1,
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2n |
故选:B.
点评:本题主要考查数列的单调性的判断,结合函数的性质是解决本题的关键,比较基础.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
抛物线x2=2y上的点到直线y=2x-3的最短距离为( )
A、
| ||||
B、
| ||||
C、2
| ||||
D、
|
已知2a+b=1,a>0,b>0,则
+
的最小值是( )
| 1 |
| a |
| 1 |
| b |
A、2
| ||
B、3-2
| ||
C、3+2
| ||
D、3+
|
已知扇形的周长为8cm,圆心角为2弧度,则该扇形的面积为( )
| A、8 | ||
B、
| ||
| C、4 | ||
| D、2 |
若双曲线与椭圆
+
=1有共同的焦点,且与椭圆相交,其中一个交点A的纵坐标为4,则双曲线的方程为( )
| x2 |
| 27 |
| y2 |
| 36 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
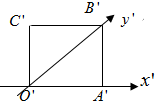 如图所示,正方形O′A′B′C′的边长2cm,它是水平放置的一个平面图形的直观图,则原图形的周长是( )
如图所示,正方形O′A′B′C′的边长2cm,它是水平放置的一个平面图形的直观图,则原图形的周长是( )| A、16cm | ||
| B、8cm | ||
C、(2+3
| ||
D、(2+2
|
设随机变量ξ服从正态分布N(0,σ2),若P(ξ<-1)=0.2,则P(-1<ξ<1)=( )
| A、0.2 | B、0.3 |
| C、0.4 | D、0.6 |
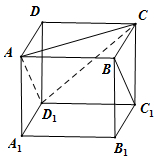 如图,ABCD-A1B1C1D1为正方体,棱长为2.下面结论中正确的结论是
如图,ABCD-A1B1C1D1为正方体,棱长为2.下面结论中正确的结论是