题目内容

20．用向量证明：若平面内的一条直线垂直于平面外的一条直线在该平面上的投影，则这两条直线垂直．

分析 画出图形，根据条件，只需把直线表示出向量，利用向量的数量积为0，证明垂直．

解答 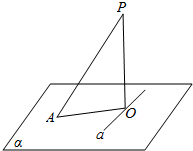证明：如图，PA、PO分别是平面α的垂线、斜线，AO是PA在平面α内的射影，
设直线a上非零向量$\overrightarrow{a}$，要证a⊥OA⇒a⊥PA，
即证$\overrightarrow{a}$•$\overrightarrow{OA}$=0⇒$\overrightarrow{a}$•$\overrightarrow{PA}$=0．
∵a?α，$\overrightarrow{a}$•$\overrightarrow{PO}$=0，
∵$\overrightarrow{a}$•$\overrightarrow{PA}$=$\overrightarrow{a}$•（$\overrightarrow{PO}$+$\overrightarrow{OA}$）=$\overrightarrow{a}$•$\overrightarrow{PO}$+$\overrightarrow{a}$•$\overrightarrow{OA}$=0+0=0．
∴a⊥PA．

点评 本题考查三垂线定理，考查向量的数量积，考查学生计算能力，属于中档题．

练习册系列答案
相关题目
10．某几何体的三视图如图所示，则该几何体的表面积为$2+\sqrt{2}$．
11．设F1，F2分别是椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（a＞b＞0）$的左、右焦点，椭圆C上一点$（\sqrt{3}，\frac{{\sqrt{2}}}{2}）$，过左焦点垂直x轴与椭圆相交所得弦长为2．
（1）求椭圆C的方程；
（2）过点E（1，0）的直线与该椭圆交于P、Q两点，且|EP|=2|EQ|，求此直线的方程；
（3）斜率为1的直线l与椭圆C交于A，B两点，O是原点，当△OAB面积最大时，求直线l的方程；
（4）若P是椭圆C上任意一点，⊙M是以PF2为直径的圆，求证：⊙M总与定圆x2+y2=a2相切．
8．已知函数f（x）=x+ex，g（x）=x+lnx，h（x）=lnx-1的零点依次为a，b，c，则a，b，c从大到小的顺序为（　　）
A．c＞b＞aB．c＞a＞bC．b＞c＞aD．a＞c＞b
15．为保护生态环境，我市某山区自2005年起开始实行退耕还林．已知2004年底该山区森林覆盖面积为a亩．
（1）设退耕还林后，森林覆盖面积的年自然增长率为2%，写出该山区的森林覆盖面积y（亩）与退耕还林年数x（年）之间的函数关系式，并求出2009年底时该山区的森林覆盖面积．
（2）如果要求到2014年底，该山区的森林覆盖面积至少是2004年底的2倍，就必须还要实行人工绿化工程．请问2014年底要达到要求，该山区森林覆盖面积的年平均增长率不能低于多少？
（参考数据：1.024=1.082，1.025=1.104，1.026=1.126，lg2=0.301，lg1.072=0.0301）
5．已知函数f（x）=$\frac{1}{3}$x3-x2+ax-a，若f（x）只有一个零点，求a的取值范围．
12．已知函数$y=|{log_{\frac{1}{2}}}x|$的定义域为$[{\frac{1}{4}，8}]$，则该函数值域为[0，3]．
9．函数$f（x）=\frac{ln（1+x）}{{\sqrt{1-x}}}$的定义域为（-1，1）．（用集合或区间表示）
10．已知x，y满足-$\frac{π}{2}$＜y＜0$＜x＜\frac{π}{2}$，且cos（$\frac{π}{4}$+x）=$\frac{1}{3}$，cos（$\frac{π}{4}$-$\frac{y}{2}$）=$\frac{\sqrt{3}}{3}$，则cos（x+$\frac{y}{2}$）=$\frac{5\sqrt{3}}{9}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网