题目内容
已知圆C1:x2+y2-4x+8y+11=0与C2:x2+y2-2x+6y+11+2m=0相交,另一圆C与x轴相切,且与圆C1关于C1、C2的公共弦所在直线L对称,求m的值及圆C的方程.
考点:直线与圆的位置关系
专题:直线与圆
分析:求出两个圆的圆心坐标,求出圆C1关于公共弦对称的点的坐标,即圆心C的坐标,利用圆C与x轴相切,建立条件关系即可求出m的值.
解答:
解:圆C1:x2+y2-4x+8y+11=0与圆C2:x2+y2-2x+6y+11+2m=0的公共弦方程为x-y+m=0,
圆C1:x2+y2-4x+8y+11=0的标准方程为(x-2)2+(y+4)2=9,圆心C1(2,-4),半径r=3,
圆C2:x2+y2-2x+6y+11+2m=0的标准方程为(x-1)2+(y+3)2=-1-2m,圆心C2(1,-3),半径r=
,
则-1-2m>0,即m<-
.
∵圆C与圆C1关于直线x-y+m=0对称,
∴圆C的半径R=3,
∵圆心C1(2,-4)关于x-y+m=0对称的点为(-4-m,2+m),
∴C(-4-m,2+m),
∵圆C与x轴相切,
∴|2+m|=3,解得m=1或m=-5,
∴m=-5,此时圆C2:(x-1)2+(y+3)2=9,半径R=3,
|C1C2|=
=
,
满足圆C1与C2相交,
∴m=-5,此时C(1,-3),
即圆C的方程为x-1)2+(y+3)2=9.
圆C1:x2+y2-4x+8y+11=0的标准方程为(x-2)2+(y+4)2=9,圆心C1(2,-4),半径r=3,
圆C2:x2+y2-2x+6y+11+2m=0的标准方程为(x-1)2+(y+3)2=-1-2m,圆心C2(1,-3),半径r=
| -1-2m |
则-1-2m>0,即m<-
| 1 |
| 2 |
∵圆C与圆C1关于直线x-y+m=0对称,
∴圆C的半径R=3,
∵圆心C1(2,-4)关于x-y+m=0对称的点为(-4-m,2+m),
∴C(-4-m,2+m),
∵圆C与x轴相切,
∴|2+m|=3,解得m=1或m=-5,
∴m=-5,此时圆C2:(x-1)2+(y+3)2=9,半径R=3,
|C1C2|=
| (2-1)2+(-3+4)2 |
| 2 |
满足圆C1与C2相交,
∴m=-5,此时C(1,-3),
即圆C的方程为x-1)2+(y+3)2=9.
点评:本题主要考查圆与圆的位置关系的应用,利用配方法求出圆心坐标是解决本题的关键,综合性较强,运算量较大.有一定的难度.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
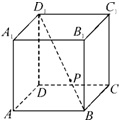 如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点的距离的不同取值有
如图,在正方体ABCD-A1B1C1D1中,P为对角线BD1的三等分点,则P到各顶点的距离的不同取值有