题目内容
有6名同学站成一排,求:
(1)甲不站排头也不站排尾有多少种不同的排法;
(2)甲不站排头,且乙不站排尾有多少种不同的排法;
(3)甲、乙、丙不相邻有多少种不同的排法.
(1)甲不站排头也不站排尾有多少种不同的排法;
(2)甲不站排头,且乙不站排尾有多少种不同的排法;
(3)甲、乙、丙不相邻有多少种不同的排法.
考点:排列、组合及简单计数问题
专题:排列组合
分析:(1)6名同学站成一排,总的排法有
中,其中甲站排头有
种,甲站排头有
种,由此能求出甲不站排头也不站排尾的排法种数.
(2)甲站排头,或乙站排尾有2
-
种不同的排法,由此能求出甲不站排头,且乙不站排尾有多少种不同的排法.
(3)利用插空法能求出甲、乙、丙不相邻有多少种不同的排法.
| A | 6 6 |
| A | 5 5 |
| A | 5 5 |
(2)甲站排头,或乙站排尾有2
| A | 5 5 |
| A | 4 4 |
(3)利用插空法能求出甲、乙、丙不相邻有多少种不同的排法.
解答:
解:(1)6名同学站成一排,总的排法有
种,
其中甲站排头有
种,甲站排头有
种,
∴甲不站排头也不站排尾有:
-2
=480种排法.
(2)甲站排头,或乙站排尾有2
-
种不同的排法,
∴甲不站排头,且乙不站排尾有:
-
+
=504种不同的排法;
(3)甲、乙、丙不相邻有
=144种不同的排法.
| A | 6 6 |
其中甲站排头有
| A | 5 5 |
| A | 5 5 |
∴甲不站排头也不站排尾有:
| A | 6 6 |
| A | 5 5 |
(2)甲站排头,或乙站排尾有2
| A | 5 5 |
| A | 4 4 |
∴甲不站排头,且乙不站排尾有:
| A | 6 6 |
| 2A | 5 5 |
| A | 4 4 |
(3)甲、乙、丙不相邻有
| A | 3 3 |
| A | 3 4 |
点评:本题考查排队种数的求法,是中档题,解题时要认真审题,注意排列数公式和组合数公式的合理运用.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
不等式2x2>3x-1的解集为( )
| A、∅ | ||
B、{x|x<-
| ||
C、(-∞,
| ||
D、{
|
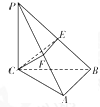 如图,已知三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,PC=BC=4,AB=2,E、F分别是PB、PA的中点.
如图,已知三棱锥P-ABC中,PC⊥平面ABC,AB⊥BC,PC=BC=4,AB=2,E、F分别是PB、PA的中点.