题目内容
已知
+
+
=
，
•
=
•
=
•
=-1．
（1）求|
|；
（2）试判断△ABC的形状，并求其面积．
| OA |
| OB |
| OC |
| 0 |
| OA |
| OB |
| OB |
| OC |
| OC |
| OA |
（1）求|
| OA |
（2）试判断△ABC的形状，并求其面积．
考点：三角形的形状判断,平面向量数量积的运算
专题：解三角形
分析：（1）由题意可得
=-
-
，平方结合已知可得
2+
2=
2+2，由
+
+
=
两边平方可得
2+
2+
2-6=0，两式综合可得
2=4，进而可得|
|=2；
（2）同理可得|
|=|
|=|
|=2，即△ABC为正三角形，易得面积．
| OA |
| OB |
| OC |
| OB |
| OC |
| OA |
| OA |
| OB |
| OC |
| 0 |
| OA |
| OB |
| OC |
| OA |
| OA |
（2）同理可得|
| OB |
| OC |
| OA |
解答：
解：（1）∵
+
+
=
，∴
=-
-
，
平方可得
2=（
+
）2=
2+
2+2
•
=
2+
2-2，
∴
2+
2=
2+2，①
由
+
+
=
两边平方可得
2+
2+
2+2
•
+2
•
+2
•
=0，
∴
2+
2+
2-6=0，②
把①代入②可得
2+
2+2-6=0，即
2=4，∴|
|=2，
（2）同理可得|
|=|
|=|
|=2，即△ABC为正三角形，
∴其面积S=
×2×2×sin60°=
| OA |
| OB |
| OC |
| 0 |
| OA |
| OB |
| OC |
平方可得
| OA |
| OB |
| OC |
| OB |
| OC |
| OB |
| OC |
| OB |
| OC |
∴
| OB |
| OC |
| OA |
由
| OA |
| OB |
| OC |
| 0 |
| OA |
| OB |
| OC |
| OA |
| OB |
| OB |
| OC |
| OC |
| OA |
∴
| OA |
| OB |
| OC |
把①代入②可得
| OA |
| OA |
| OA |
| OA |
（2）同理可得|
| OB |
| OC |
| OA |
∴其面积S=
| 1 |
| 2 |
| 3 |
点评：本题考查三角形形状的判断，涉及向量的数量积的运算，属中档题．
练习册系列答案
相关题目
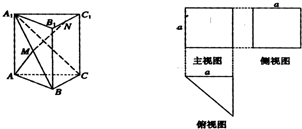一个多面体的三视图及直观图如图所示，M、N分别是A1B、B1C1的中点．