题目内容
给定抛物线C:y2=4x,过点A(-1,0)的斜率为k的直线与C相交于M,N两点.
(1)MN的中点在直线x=3上,求k的值;
(2)折
=λ
,k∈[
,
],求λ的取值范围.
(1)MN的中点在直线x=3上,求k的值;
(2)折
| AM |
| AN |
| ||
| 2 |
| ||
| 3 |
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)直线MN的方程为:y=k(x+1),M(x1,y1),N(x2,y2).与抛物线方程联立k2x2+(2k2-4)x+k2=0,k≠0.利用根与系数的关系、中点坐标公式即可得出.
(2)利用
=λ
,可得x1+1=λ(x2+1),利用根与系数的关系可得x1+x2=
,x1x2=1联立.化为k2=
,利用k∈[
,
],即可得出.
(2)利用
| AM |
| AN |
| 4-2k2 |
| k2 |
| 4λ |
| (1+λ)2 |
| ||
| 2 |
| ||
| 3 |
解答:
解:(1)直线MN的方程为:y=k(x+1),M(x1,y1),N(x2,y2).
联立
,化为k2x2+(2k2-4)x+k2=0,k≠0.
∴x1+x2=
=2×3,x1x2=1.
解得k=±
.
(2)∵
=λ
,x1+1=λ(x2+1),
与x1+x2=
,x1x2=1联立.
可得k2=
,
∵k∈[
,
],
∴
≤
≤
,
解得λ∈[3-2
,2-
]∪[2+
,3+2
].
∴λ的取值范围是[3-2
,2-
]∪[2+
,3+2
].
联立
|
∴x1+x2=
| 4-2k2 |
| k2 |
解得k=±
| ||
| 2 |
(2)∵
| AM |
| AN |
与x1+x2=
| 4-2k2 |
| k2 |
可得k2=
| 4λ |
| (1+λ)2 |
∵k∈[
| ||
| 2 |
| ||
| 3 |
∴
| 1 |
| 2 |
| 4λ |
| (1+λ)2 |
| 2 |
| 3 |
解得λ∈[3-2
| 2 |
| 3 |
| 3 |
| 2 |
∴λ的取值范围是[3-2
| 2 |
| 3 |
| 3 |
| 2 |
点评:本题考查了直线与抛物线相交问题转化为方程联立可得根与系数的关系、向量运算、不等式的性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数y=
的定义域为( )
| 4x+2 |
A、{x|x≥-
| ||
B、(-
| ||
C、(-∞,-
| ||
D、{x|x≤-
|
把一根长度为5的铁丝截成任意长的3段,则能构成三角形的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
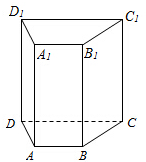 如图,直四棱柱ABCD-A1B1C1D1,底面ABCD为梯形AB∥CD,ABC=90°,BC=CD=2AB=2.
如图,直四棱柱ABCD-A1B1C1D1,底面ABCD为梯形AB∥CD,ABC=90°,BC=CD=2AB=2.