题目内容
17.抛物线y2=4x的焦点到双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1的一条渐近线的距离是$\frac{\sqrt{3}}{2}$,则双曲线的虚轴长是( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 3 | D. | 6 |
分析 先确定抛物线的焦点位置,进而可确定抛物线的焦点坐标,再由题中条件求出双曲线的渐近线方程,再代入点到直线的距离公式即可求出结论.
解答 解:抛物线y2=4x的焦点在x轴上,且p=2,
∴抛物线y2=4x的焦点坐标为(1,0),
由题得:双曲线双曲线x2-$\frac{{y}^{2}}{{b}^{2}}$=1的渐近线方程为bx±y=0,
∴抛物线的焦点到渐近线的距离d=$\frac{b}{\sqrt{1+{b}^{2}}}$=$\frac{\sqrt{3}}{2}$,
解得b=$\sqrt{3}$,
∴则双曲线的虚轴长是2b=2$\sqrt{3}$,
故选:B
点评 本题考查抛物线的性质,考查双曲线的基本性质,解题的关键是定型定位,属于基础题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
7.“金导电、银导电、铜导电、锡导电,所以一切金属都导电”.此推理方法是( )
| A. | 完全归纳推理 | B. | 归纳推理 | C. | 类比推理 | D. | 演绎推理 |
8.已知f(x)=4x3-6x2+m(m为常数)在[-2,1]上有最大值5,那么此函数在[-2,1]上的最小值是( )
| A. | 3 | B. | -49 | C. | -52 | D. | -51 |
5.执行如图所示的程序框图,若输入p=2017,则输出i的值为( )
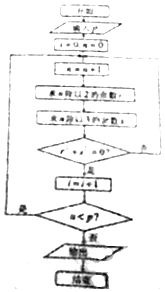

| A. | 335 | B. | 336 | C. | 337 | D. | 338 |
12.若直线ax-by+2=0 (a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )
| A. | $\frac{3}{2}$+$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{2}$+2$\sqrt{2}$ |