题目内容
13.自原点O作圆(x-1)2+y2=1的不重合的两弦OA,OB,且|OA|•|OB|=2,若不论A,B两点的位置怎样,直线AB恒切与一个定圆,请求出定圆的方程.分析 设AB边上的高为h,则△AOB的面积S=$\frac{1}{2}$|AB|•h,再利用S=$\frac{1}{2}$|OA|•|OB|•sin∠AOB,即可得到结论.
解答 解:由题意,圆(x-1)2+y2=1是△AOB的外接圆,半径为1,根据正弦定理:|AB|=2Rsin∠AOB=2sin∠AOB,
设AB边上的高为h,则△AOB的面积$S=\frac{1}{2}|AB|•h=h•sin∠AOB$
∵$S=\frac{1}{2}|OA|•|OB|•sin∠AOB$=$\frac{1}{2}×2×sin∠AOB$
∴h=1为定值,
即O到AB的距离为定值1,
∴直线AB与以原点为圆心,1为半径的圆相切,圆的方程为x2+y2=1.
点评 本题考查直线与圆的位置关系,考查圆的方程,考查学生的计算能力,属于基础题.

练习册系列答案
相关题目
3.原点与极点重合,x轴正半轴与极轴重合,则点(2,-2$\sqrt{3}$)的极坐标是( )
| A. | (4,$\frac{π}{3}$) | B. | (4,$\frac{4π}{3}$) | C. | (-4,-$\frac{2π}{3}$) | D. | (4,-$\frac{2π}{3}$) |
4.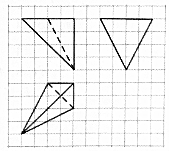 如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )
 如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某三棱锥的三视图,则该三棱锥的体积为( )| A. | $\frac{8}{3}$ | B. | $\frac{16}{3}$ | C. | $\frac{32}{3}$ | D. | 16 |
1.如果x2+(y-k+1)2=2表示圆心在y轴负半轴上的圆,那么实数k的一个可能值是( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
5.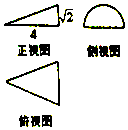 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
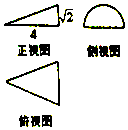 一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )
一个几何体的三视图及尺寸如图所示,其中正视图是直角三角形,侧视图是半圆,俯视图是等腰三角形,该几何体的体积为( )| A. | $\frac{4}{3}$π | B. | $\frac{4\sqrt{2}}{3}$π | C. | 4π | D. | 4$\sqrt{2}$π |
2.设集合A={x|x2-1<0},B={y|y=2x,x∈A},则A∩B=( )
| A. | (0,1) | B. | ($\frac{1}{2}$,1) | C. | (-1,2) | D. | (-1,+∞) |