题目内容
已知a，b均为正数，且a+b=1，证明：
（1）（ax+by）2≤ax2+by2
（2）（a+
）2+（b+
）2≥
．
（1）（ax+by）2≤ax2+by2
（2）（a+
| 1 |
| a |
| 1 |
| b |
| 25 |
| 2 |
考点：不等式的证明
专题：证明题
分析：（1）将所证的关系式作差（ax+by）2-（ax2+by2）=a（a-1）x2+b（b-1）y2+2abxy利用a+b=1，整理，可得a（a-1）x2+b（b-1）y2+2abxy=-ab（x-y）2≤0，当且仅当x=y时等号成立；
（2）将所证的不等式左端展开，转化为(a+
)2+(b+
)2=4+a 2+b2+(
+
)，进一步整理后，利用基本不等式即可证得结论成立．
（2）将所证的不等式左端展开，转化为(a+
| 1 |
| a |
| 1 |
| b |
| 1 |
| a2 |
| 1 |
| b2 |
解答：
证明：（1））（ax+by）2-（ax2+by2）=a（a-1）x2+b（b-1）y2+2abxy，
因为a+b=1，
所以a-1=-b，b-1=-a，又a，b均为正数，
所以a（a-1）x2+b（b-1）y2+2abxy=-ab（x2+y2-2xy）=-ab（x-y）2≤0，当且仅当x=y时等号成立；
（2）(a+
)2+(b+
)2=4+a 2+b2+(
+
)
=4+a2+b2+
+
=4+a2+b2+1+
+
+
+
+1
=4+(a2+b2)+2+2(
+
)+(
+
)≥4+
+2+4+2=
．
当且仅当a=b时等号成立．
因为a+b=1，
所以a-1=-b，b-1=-a，又a，b均为正数，
所以a（a-1）x2+b（b-1）y2+2abxy=-ab（x2+y2-2xy）=-ab（x-y）2≤0，当且仅当x=y时等号成立；
（2）(a+
| 1 |
| a |
| 1 |
| b |
| 1 |
| a2 |
| 1 |
| b2 |
=4+a2+b2+
| (a+b)2 |
| a2 |
| (a+b)2 |
| b2 |
| 2b |
| a |
| b2 |
| a2 |
| a2 |
| b2 |
| 2a |
| b |
=4+(a2+b2)+2+2(
| b |
| a |
| a |
| b |
| b2 |
| a2 |
| a2 |
| b2 |
| (a+b)2 |
| 2 |
| 25 |
| 2 |
当且仅当a=b时等号成立．
点评：本题考查不等式的证明，着重考查作差法的应用，突出考查等价转化思想与逻辑推理能力，属于难题．
练习册系列答案
相关题目
从高三年级随机抽取100名学生，将他们的某次考试数学成绩绘制成频率分布直方图．由图中数据可知成绩在[130，140）内的学生人数为（ ）| A、20 | B、25 | C、30 | D、35 |
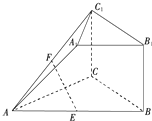如图所示的几何体中，四边形BB1C1C是矩形，BB1⊥平面ABC，CA=CB，A1B1∥AB，AB=2A1B1，E，F分别是AB，AC1的中点．
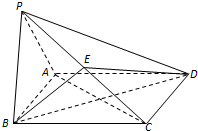如图，在四棱锥P-ABCD中，底面ABCD为矩形，平面PAB⊥平面ABCD，PA⊥PB，BP=BC，E为PC的中点．