题目内容
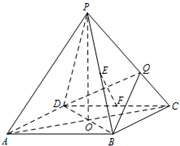 如图,正四棱锥P-ABCD的高为PO,PO=AB=2.E,F分别是棱PB,CD的中点,Q是棱PC上的点.
如图,正四棱锥P-ABCD的高为PO,PO=AB=2.E,F分别是棱PB,CD的中点,Q是棱PC上的点.(1)求证:EF∥平面PAD;
(2)若PC⊥平面QDB,求PQ.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)取PA中点M,连结ME,MD,根据中位线的性质知ME∥AB,DF∥AB,进而推断出ME∥DF,利用ME=
AB,DF=
AB,推断出ME=DF,进而可证明出四边形EFDM是平行四边形,知EF∥MD,最后由线面的判定定理证明出EF∥平面PAD.
(2)连结OQ,利用线面垂直性质推断出分别推断出PC⊥OQ,PO⊥OC,由正方形的边长得到OC,然后利用勾股定理求得PC,最后求得PQ.
| 1 |
| 2 |
| 1 |
| 2 |
(2)连结OQ,利用线面垂直性质推断出分别推断出PC⊥OQ,PO⊥OC,由正方形的边长得到OC,然后利用勾股定理求得PC,最后求得PQ.
解答:
(1)证明:取PA中点M,连结ME,MD,
由条件,得ME∥AB,DF∥AB,
∴ME∥DF,
且ME=
AB,DF=
AB,
∴ME=DF,
∴四边形EFDM是平行四边形.
则EF∥MD,
由MD?平面PAD,EF不属于面PAD,
∴EF∥平面PAD.
(2)连结OQ,
∵PC⊥平面QDB,OQ?平面QDB,
∴PC⊥OQ,
∵PO⊥平面ABCD,OC?平面ABCD,
∴PO⊥OC,
∵PO=2,
∴PC=
=
则PQ=PO•cos∠CPO=2•
=

由条件,得ME∥AB,DF∥AB,
∴ME∥DF,
且ME=
| 1 |
| 2 |
| 1 |
| 2 |
∴ME=DF,
∴四边形EFDM是平行四边形.
则EF∥MD,
由MD?平面PAD,EF不属于面PAD,
∴EF∥平面PAD.
(2)连结OQ,
∵PC⊥平面QDB,OQ?平面QDB,
∴PC⊥OQ,
∵PO⊥平面ABCD,OC?平面ABCD,
∴PO⊥OC,
∵PO=2,
∴PC=
| OP2+OC2 |
| 6 |
则PQ=PO•cos∠CPO=2•
| 2 | ||
|
2
| ||
| 3 |

点评:本题主要考查了线面平行和线面垂直的性质和判定定理的运用.考查了学生空间观察能力和基础的综合运用.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案 应用题作业本系列答案
应用题作业本系列答案
相关题目
已知x1、x2是函数f(x)=
-3的两个零点,若a<x1<x2,则f(a)的值是( )
| ex |
| x |
| A、f(a)=0 |
| B、f(a)>0 |
| C、f(a)<0 |
| D、f(a)的符号不确定 |