题目内容
已知f（x）=ln（2x+1），y=f（x）和y=g（x）的图象关于直线y=2x+1对称，M，N分别为y=f（x）和y=g（x）上的点，则|MN|的最小值为 ．
考点：对数函数的图像与性质
专题：函数的性质及应用
分析：根据题意可判断M，N分别为y=f（x）和y=g（x）上的点，|MN|的最小值时，即为M到直线y=2x+1的最近的位置，运用导数判断即可．
解答：
解：
f（x）=ln（2x+1），x＞-
，
f′（x）=
，
∵直线y=2x+1，
∴
=2，
x0=0，y0=ln（2×0+1）=0，
点（0，0）到直线y=2x+1的距离为函数f（x）=ln（2x+1）上的点到直线y=2x+1最小，
∴d=
，
∵y=f（x）和y=g（x）的图象关于直线y=2x+1对称，M，N分别为y=f（x）和y=g（x）上的点，
∴M（0，0）符合题意，
∴|MN|的最小值为
，
故答案为：
．
f（x）=ln（2x+1），x＞-
| 1 |
| 2 |
f′（x）=
| 2 |
| 2x+1 |
∵直线y=2x+1，
∴
| 2 |
| 2x0+1 |
x0=0，y0=ln（2×0+1）=0，
点（0，0）到直线y=2x+1的距离为函数f（x）=ln（2x+1）上的点到直线y=2x+1最小，
∴d=
| 1 | ||
|
∵y=f（x）和y=g（x）的图象关于直线y=2x+1对称，M，N分别为y=f（x）和y=g（x）上的点，
∴M（0，0）符合题意，
∴|MN|的最小值为
2
| ||
| 5 |
故答案为：
2
| ||
| 5 |
点评：本题考查了函数的图象，导数的运用，判断最小值问题，综合运用各种知识，属于难度较大的题目，关键是分析的出求解思路．
练习册系列答案
阅读快车系列答案
相关题目
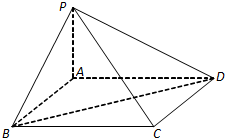如图，在四棱锥P-ABCD中，底面ABCD是菱形，且PB=PD．
已知抛物线y2=4x内一定点E（m，0），（m＞0），过点E作斜率分别为k1，k2的两条直线，交抛物线于A、B和C、D，且M，N分别是线段AB、CD的中点．
如图所示，圆O的直径为BD，过圆上一点A作圆O的切线AE，过点D作DE⊥AE于点E，延长ED与圆O交于点C．