题目内容
一只半径为R的球放在桌面上,桌面上一点A的正上方相距(
+1)R处有一点光源O,OA与球相切,则球在桌面上的投影------椭圆的离心率为 .
| 3 |
考点:平面与圆柱面的截线
专题:圆锥曲线的定义、性质与方程
分析:根据圆曲线的第一定义,作出过圆锥的轴与椭圆长轴AA′的截面,可得直角三角形AOA′,结合已知求出椭圆的a值,再根据椭圆的几何性质,求出c,即可求出椭圆的离心率.
解答:
解:如图是过圆锥的轴与椭圆长轴AA′的截面,
ED两点为过点O引圆D的两条切线与圆D的切点,
∵OA=(
+1)R,
故在Rt△OBE中,
OE=
R,BE=R,
则tan∠EOB=
,
即∠EOB=30°,
故∠EOB=60°,即∠AOA′=60°,
故AA′=2a=
OA=(3+
)R,即a=
R,
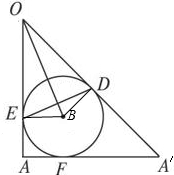
根据圆锥曲线的定义,
可得球与长轴AA′的切点是椭圆的焦点F,
根据椭圆的几何性质,AF是焦点到长轴顶点的距离AF=a-c=R,
∴c=
R=
a,
所求椭圆的离心率e=
=
,
故答案为:
ED两点为过点O引圆D的两条切线与圆D的切点,
∵OA=(
| 3 |
故在Rt△OBE中,
OE=
| 3 |
则tan∠EOB=
| ||
| 3 |
即∠EOB=30°,
故∠EOB=60°,即∠AOA′=60°,
故AA′=2a=
| 3 |
| 3 |
3+
| ||
| 2 |

根据圆锥曲线的定义,
可得球与长轴AA′的切点是椭圆的焦点F,
根据椭圆的几何性质,AF是焦点到长轴顶点的距离AF=a-c=R,
∴c=
1+
| ||
| 2 |
| ||
| 3 |
所求椭圆的离心率e=
| c |
| a |
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题以空间的圆锥为载体,考查了圆锥曲线的形成过程,同时考查了椭圆的基本量,属于中档题.深刻理解空间位置关系和椭圆的定义与性质,是解决本题的关键.

练习册系列答案
相关题目
设m,n,l是空间中三条不重合的直线,则下列命题中正确的是( )
| A、若m∥n,n⊥l,则m⊥l |
| B、若m⊥n,n⊥l,则m∥l |
| C、若m,n共面,n与l共面,则m与l共面 |
| D、若m,n异面,n与l异面,则m与l异面 |
已知{an}是等比数列,a1=2,a4=16,则公比q等于( )
A、
| ||
B、
| ||
| C、2 | ||
| D、4 |
已知x与y之间的一组数据如下表所示,则y与x的线性回归方程y=bx+a必经过点( )
| x | 1 | 2 | 3 | 5 | 6 | 7 |
| y | 1.1 | 1.7 | 5.6 | 6.2 | 7.4 | 9.5 |
| A、(4,5.35) |
| B、(4,5.25) |
| C、(5,5.591) |
| D、(3,5.6) |
 已知函数f(x)=2sin(ωx+φ),x∈R(其中ω>0,|φ|<
已知函数f(x)=2sin(ωx+φ),x∈R(其中ω>0,|φ|<