题目内容
15.设等差数列{an}的前n项和为Sn,若a4=4,则S7=28.分析 由已知得S7=$\frac{7}{2}$(a1+a7)=2a4,由此能求出结果.
解答 解:∵等差数列{an}的前n项和为Sn,a4=4,
∴S7=$\frac{7}{2}$(a1+a7)=7a4=28.
故答案为:28.
点评 本题考查等差数列的前2018项和的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
20.已知i为虚数单位,复数z满足z(1-i)=1+i,则z的共轭复数是( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
7.下列函数中,既是偶函数又在(0,+∞)上单调递减的是( )
| A. | y=-x | B. | y=cosx | C. | y=${x^{\frac{2}{5}}}$ | D. | y=-x2 |
5.化简sin2(2π-α)+cos(π+α)cos(π-α)+1( )
| A. | 0 | B. | 2sin2α+1 | C. | 2cos2α+1 | D. | 2 |
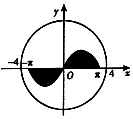 如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点A,则点A落在区域M外的概率是1-$\frac{1}{4π}$.
如图,圆O:x2+y2=16内的正弦曲线y=sinx,x∈[-π,π]与x轴围成的区域记为M(图中阴影部分),随机向圆O内投一个点A,则点A落在区域M外的概率是1-$\frac{1}{4π}$.