题目内容
已知θ∈(
,π),sin
-cos
=
,则cosθ= .
| π |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| ||
| 5 |
考点:二倍角的余弦
专题:三角函数的求值
分析:由θ∈(
,π),sin
-cos
=
,求出sin2θ,然后求出cos2θ.
| π |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| ||
| 5 |
解答:
解:∵θ∈(
,π),sin
-cos
=
,∴1-sinθ=
,
∴sinθ=
,
∵θ∈(
,π),∴cosθ=-
=-
.
故答案为:-
.
| π |
| 2 |
| θ |
| 2 |
| θ |
| 2 |
| ||
| 5 |
| 2 |
| 5 |
∴sinθ=
| 3 |
| 5 |
∵θ∈(
| π |
| 2 |
| 1-sin2θ |
| 4 |
| 5 |
故答案为:-
| 4 |
| 5 |
点评:本题考查二倍角的余弦,解题时要认真审题,仔细解答,注意三角函数的符号的正确选取.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f(x)=ex-x2+8x,则在下列区间中f(x)必有零点的是( )
| A、(-2,-1) |
| B、(-1,0) |
| C、(0,1) |
| D、(1,2) |
已知A,B两地相距150km,某人驾驶汽车以60km/h的速度从A地到达B地,在B地停留1h后再以50km/h的速度返回A地并停在A地,将汽车与A地的距离s(单位:km)表示成时间t(单位:h)的函数为( )
| A、s=60t | |||||||||||
B、s=
| |||||||||||
C、s=
| |||||||||||
| D、s=60t+50 |
若θ∈[0,
],sin2θ=
,则cosθ=( )
| π |
| 4 |
2
| ||
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
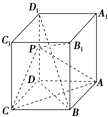 如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点
如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点