题目内容

已知f（x）=x2+3x，求f[f（1）]和f（x+1）．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：根据f（x）解析式求出f（1），并带入f（x）解析式求出f[f（1）]，将x+1带入f（x）解析式即可求出f（x+1）．
解答： 解：f[f（1）]=（f（1））2+3f（1）=16+12=28；
f（x+1）=（x+1）2+3（x+1）=x2+5x+4．
点评：考查已知f（x）解析式求f[f（a）]或求f[g（x）]的方法．
练习册系列答案
相关题目
数列{an}的首项a1=1，前n项和Sn满足2kSn-（2k+1）Sn-1=2k（常数k＞0，n=2，3，4，…）
（1）求证：数列{an}是等比数列；
（2）设数列{an}的公比为f（k），作数列{bn}，使b1=3，bn=f（
1
bn-1
）（n=2，3，4，…）求数列{bn}的通项公式；
（3）设cn=bn-2，若存在m∈N*，使
lim
n→∞
（cmcm+1+cm+1cm+2+…+cncn+1）＜
1
2007
，试求m的最小值．
已知集合A={x|x2-2x-3＜0}，B={x|x2+（a+1）x+2a＜0}且满足A?B，求a的取值范围．
已知数列{an}满足（n-1）an+1=（n+1）（an-1）且a2=6，求{an}通项公式．
已知f（x）=ax+b，且f（2）=-2，f（6）=0，则f（8）=
 
．
过点（3，1）作圆（x+1）2+y2=1的两条切线，切点分别为A，B，则直线AB的方程为（　　）
A、2x+y-
9
2
=0
B、2x-y-
9
2
=0
C、4x-y-
9
2
=0
D、4x+y-
9
2
=0
已知函数y=
1
2
cos2x+
3
2
sinxcosx+1，x∈R．
（1）当函数y取得最大值时，求自变量x的集合；
（2）当x∈[0，π]时，求该函数的单调增区间．
已知f（x）为一次函数，且y随x值增大而增大，若f[f（x）]=4x+6，f（x）的解析式
 
．
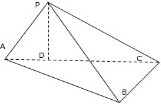如图，在三棱锥P-ABC中，PD⊥面ABC于点D，且点D在AC上，PA=PB=PC=3，设AB=BC=2
3
，求AC与平面BPC所成角．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网