题目内容
已知二次函数f(x)满足f(x+1)-f(x)=2x+3,且f(0)=4.
(1)求f(x)的解析式;
(2)求f(x)在[-3,4]上的值域.
(1)求f(x)的解析式;
(2)求f(x)在[-3,4]上的值域.
考点:二次函数在闭区间上的最值
专题:计算题,待定系数法,函数的性质及应用
分析:(1)据二次函数的形式设出f(x)的解析式,将已知条件代入,列出方程,令方程两边的对应系数相等解得.
(2)讨论对称轴与区间的关系,即可得到最值,进而求得值域.
(2)讨论对称轴与区间的关系,即可得到最值,进而求得值域.
解答:
解:(1)设y=f(x)=ax2+bx+c
∵f(0)=c=4,f(x+1)-f(x)=2x+3,
∴a(x+1)2+b(x+1)+c-(ax2+bx+c)=2x+3,
∴2a=2,a+b=3,解得a=1,b=2,
则函数f(x)的表达式为f(x)=x2+2x+4;
(2)由于f(x)=x2+2x+4的对称轴为x=-1,
而-1∈[-3,4],
则f(x)的最小值为f(-1)=1-2+4=3,
当x=4时,f(x)取最大值,且为f(4)=16+8+4=28,
故f(x)在[-3,4]上的值域为[3,28].
∵f(0)=c=4,f(x+1)-f(x)=2x+3,
∴a(x+1)2+b(x+1)+c-(ax2+bx+c)=2x+3,
∴2a=2,a+b=3,解得a=1,b=2,
则函数f(x)的表达式为f(x)=x2+2x+4;
(2)由于f(x)=x2+2x+4的对称轴为x=-1,
而-1∈[-3,4],
则f(x)的最小值为f(-1)=1-2+4=3,
当x=4时,f(x)取最大值,且为f(4)=16+8+4=28,
故f(x)在[-3,4]上的值域为[3,28].
点评:本题考查利用待定系数法求函数解析式,考查二次函数在闭区间上的值域,注意对称轴与区间的关系,考查运算能力,属于中档题.

练习册系列答案
相关题目
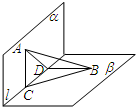 已知平面α⊥平面β,α∩β=l,A∈α,B∈β,AC⊥l,垂足为C,BD⊥l,垂足为D(点C,D不重合),若AC>BD,则( )
已知平面α⊥平面β,α∩β=l,A∈α,B∈β,AC⊥l,垂足为C,BD⊥l,垂足为D(点C,D不重合),若AC>BD,则( )| A、AD>BC,∠ABC>∠BAD |
| B、AD>BC,∠ABC<∠BAD |
| C、AD<BC,∠ABC>∠BAD |
| D、AD<BC,∠ABC<∠BAD |
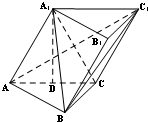 如图所示,已知三棱柱ABC-A1B1C1,点A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,BA1⊥AC1.
如图所示,已知三棱柱ABC-A1B1C1,点A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,BA1⊥AC1.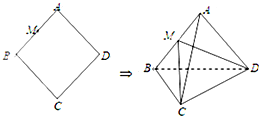 在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为
在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后使∠ADC的余弦值为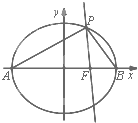 已知椭圆C的中心在坐标原点,右焦点为F(1,0),A,B是椭圆的左、右顶点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为
已知椭圆C的中心在坐标原点,右焦点为F(1,0),A,B是椭圆的左、右顶点,P是椭圆C上异于A,B的动点,且△APB面积的最大值为