题目内容
已知x∈(0,1)时,不等式(
)3ax-1>(
)ax-x2恒成立,求实数a的范围.
| 1 |
| 2 |
| 1 |
| 2 |
考点:指、对数不等式的解法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:运用指数函数的单调性,可得3ax-1<ax-x2对x∈(0,1)恒成立,即有2a<
-x,判断
-x的单调性及范围,
即可得到a的范围.
| 1 |
| x |
| 1 |
| x |
即可得到a的范围.
解答:
解:不等式(
)3ax-1>(
)ax-x2恒成立,
即为3ax-1<ax-x2对x∈(0,1)恒成立,
即有2a<
-x,
由于
-x在(0,1)递减,即有
-x>0,
则有2a≤0,即有a≤0.
| 1 |
| 2 |
| 1 |
| 2 |
即为3ax-1<ax-x2对x∈(0,1)恒成立,
即有2a<
| 1 |
| x |
由于
| 1 |
| x |
| 1 |
| x |
则有2a≤0,即有a≤0.
点评:本题考查函数恒成立问题,考查函数的单调性的运用,考查参数分离法,属于中档题.

练习册系列答案
相关题目
函数y=
的值域是( )
| 1-2x |
| A、(0,1] |
| B、[0,1) |
| C、(-∞,0] |
| D、[0,+∞) |
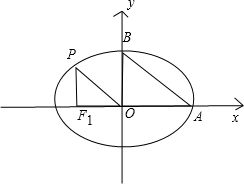 如图,从椭圆
如图,从椭圆