题目内容
(文)已知椭圆
+
=1的一条弦的中点为P(4,2),求此弦所在直线l的方程.
| x2 |
| 36 |
| y2 |
| 9 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:设弦的端点坐标为(x1,y1),(x2,y2),则x1+x2=8,y1+y2=4,代入椭圆方程可得,
+
=1①,
+
=1,两式相减变形可求得直线斜率,利用点斜式可得直线方程,注意检验.
| x12 |
| 36 |
| y12 |
| 9 |
| x22 |
| 36 |
| y22 |
| 9 |
解答:
解:设弦的端点坐标为(x1,y1),(x2,y2),
则x1+x2=8,y1+y2=4,
代入椭圆方程可得,
+
=1①,
+
=1②,
①-②得,
+
=0,
整理可得
=-
=-
,
即kAB=-
,
由点斜式可得直线方程为:y-2=-
(x-4),即x+2y-8=0,
经检验符合题意,
此弦所在直线l的方程:x+2y-8=0.
则x1+x2=8,y1+y2=4,
代入椭圆方程可得,
| x12 |
| 36 |
| y12 |
| 9 |
| x22 |
| 36 |
| y22 |
| 9 |
①-②得,
| x12-x22 |
| 36 |
| y12-y22 |
| 9 |
整理可得
| y1-y2 |
| x1-x2 |
| x1+x2 |
| 4(y1+y2) |
| 1 |
| 2 |
即kAB=-
| 1 |
| 2 |
由点斜式可得直线方程为:y-2=-
| 1 |
| 2 |
经检验符合题意,
此弦所在直线l的方程:x+2y-8=0.
点评:本题考查直线与椭圆的位置关系,属中档题,涉及弦中点问题常采取“平方差法”解决.

练习册系列答案
相关题目
已知中心在原点的双曲线,其右焦点为F(3,0),且F到其中一条渐近线的距离为
,则该双曲线的方程为( )
| 5 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知变量x,y满足约束条件
,若目标函数z=y+ax仅在点(5,3)处取得最小值,则实数a的取值范围为( )
|
| A、(-∞,-1) | ||
| B、(0,+∞) | ||
C、(
| ||
| D、(1,+∞) |
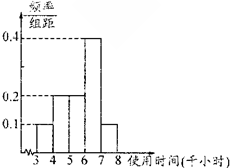 节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明治疗越好.若使用时间小于4千小时的产品为不合格产品;使用时间在4千小时到6千小时(不含6千小时)的产品为合格品;使用时间大于或等于6千小时的产品为优质品.某节能灯生产厂家为了解同一类型号的某批次产品的质量情况,随机抽取了部分产品作为样本,得到实验结果的频率直方图如图所示.若上述实验结果中使用时间落入各组的频率作为相应的概率.
节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明治疗越好.若使用时间小于4千小时的产品为不合格产品;使用时间在4千小时到6千小时(不含6千小时)的产品为合格品;使用时间大于或等于6千小时的产品为优质品.某节能灯生产厂家为了解同一类型号的某批次产品的质量情况,随机抽取了部分产品作为样本,得到实验结果的频率直方图如图所示.若上述实验结果中使用时间落入各组的频率作为相应的概率.