题目内容
16.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{(a+3)^{2}}$=1(a>0)的一条渐近线方程为y=2x,则a=3.分析 根据题意,由双曲线的方程可得其渐近线方程为y=±$\frac{a+3}{a}$x,结合题意可得$\frac{a+3}{a}$=2,解可得a的值,即可得答案.
解答 解:根据题意,双曲线的方程为:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{(a+3)^{2}}$=1(a>0),
则其渐近线方程为:y=±$\frac{a+3}{a}$x,
若其一条渐近线方程为y=2x,则有$\frac{a+3}{a}$=2,
解可得a=3;
故答案为:3.
点评 本题考查双曲线的几何性质,关键是用a表示出双曲线的渐近线方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.某地区以“绿色出行”为宗旨开展“共享单车”业务.该地有a,b两种“共享单车”(以下简称a型车,b型车).某学习小组7名同学调查了该地区共享单车的使用情况.
(Ⅰ)某日该学习小组进行一次市场体验,其中4人租到a型车,3人租到b型车.如果从组内随机抽取2人,求抽取的2人中至少有一人在市场体验过程中租到a型车的概率;
(Ⅱ)根据已公布的2016年该地区全年市场调查报告,小组同学发现3月,4月的用户租车情况城现如表使用规律.例如,第3个月租a型车的用户中,在第4个月有60%的用户仍租a型车.
若认为2017年该地区租用单车情况与2016年大致相同.已知2017年3月该地区租用a,b两种车型的用户比例为1:1,根据表格提供的信息,估计2017年4月该地区租用两种车型的用户比例.
(Ⅰ)某日该学习小组进行一次市场体验,其中4人租到a型车,3人租到b型车.如果从组内随机抽取2人,求抽取的2人中至少有一人在市场体验过程中租到a型车的概率;
(Ⅱ)根据已公布的2016年该地区全年市场调查报告,小组同学发现3月,4月的用户租车情况城现如表使用规律.例如,第3个月租a型车的用户中,在第4个月有60%的用户仍租a型车.
第3个月 第4个月 | 租用a型车 | 租用b型车 |
| 租用a型车 | 60% | 50% |
| 租用b型车 | 40% | 50% |
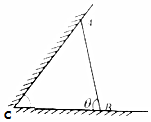 某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ
某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ