题目内容
4.点A、B、C、D在同一个球的球面上,$AB=BC=2,AC=2\sqrt{2}$,若四面体ABCD体积的最大值为$\frac{4}{3}$,则该球的表面积为9π.分析 根据三棱锥的特征,判定外接球的球心,求出球的半径,即可求出球的表面积.
解答 解:根据题意知,△ABC是一个直角三角形,其面积为2.其所在球的小圆的圆心在斜边AC的中点上,设小圆的圆心为Q,
四面体ABCD的体积的最大值,由于底面积S△ABC不变,高最大时体积最大,
所以,DQ与面ABC垂直时体积最大,最大值为$\frac{1}{2}$×S△ABC×DQ=$\frac{4}{3}$,
S△ABC=$\frac{1}{2}$AC•BQ=$\frac{1}{2}×2\sqrt{2}×\sqrt{2}$=2.,∴DQ=2,如图.
设球心为O,半径为R,则在直角△AQO中,OA2=AQ2+OQ2,即R2=($\sqrt{2}$)2+(2-R)2,∴R=$\frac{3}{2}$,
则这个球的表面积为:S=4π($\frac{3}{2}$)2=9π;
故答案为:9π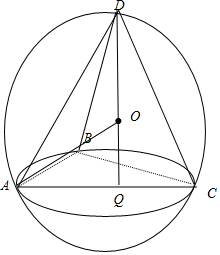
点评 本题考查的知识点是球内接多面体,球的表面积,其中分析出何时四面体ABCD的体积的最大值,是解答的关键.属于中档题.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
12.为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前7次考试的数学成绩x、物理成绩y进行分析.下面是该生7次考试的成绩.
(Ⅰ)他的数学成绩与物理成绩哪个更稳定?请给出你的说明;
(Ⅱ)已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程
(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
| 数学 | 108 | 103 | 137 | 112 | 128 | 120 | 132 |
| 物理 | 74 | 71 | 88 | 76 | 84 | 81 | 86 |
(Ⅱ)已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程
(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
19.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$过点(3,2),当a2+b2取得最小值时,椭圆的离心率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{{\sqrt{3}}}{3}$ |