题目内容
1.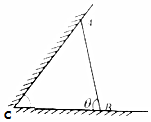 某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ
某动物园要为刚入园的小动物建造一间两面靠墙的三角形露天活动室,地面形状如图所示,已知已有两面墙的夹角为$\frac{π}{3}$(∠ACB=$\frac{π}{3}$),墙AB的长度为6米,(已有两面墙的可利用长度足够大),记∠ABC=θ(1)若θ=$\frac{π}{4}$,求△ABC的周长(结果精确到0.01米);
(2)为了使小动物能健康成长,要求所建的三角形露天活动室面积△ABC的面积尽可能大,问当θ为何值时,该活动室面积最大?并求出最大面积.
分析 (1)在△ABC中,由正弦定理可得AC,BC,即可求△ABC的周长;
(2)利用余弦定理列出关系式,将c,cosC的值代入并利用基本不等式求出ab的最大值,利用三角形的面积公式求出面积的最大值,以及此时θ的值.
解答 解:(1)在△ABC中,由正弦定理可得AC=$\frac{6•\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=2$\sqrt{6}$,BC=$\frac{6sin75°}{\frac{\sqrt{3}}{2}}$=3$\sqrt{2}$+$\sqrt{6}$,
∴△ABC的周长为6+3$\sqrt{2}$+3$\sqrt{6}$≈17.60米
(2)在△ABC中,由余弦定理:c2=602=a2+b2-2abcos60°,
∴a2+b2-ab=36,
∴36+ab=a2+b2≥2ab,即ab≤36,
∴S△ABC=$\frac{1}{2}$AC•BC•sin$\frac{π}{3}$=$\frac{\sqrt{3}}{4}$ab≤9$\sqrt{3}$,
此时a=b,△ABC为等边三角形,
∴θ=60°,(S△ABC)max=9$\sqrt{3}$.
点评 此题考查了正弦定理、余弦定理,基本不等式的应用,熟练掌握余弦定理是解本题的关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
12.为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前7次考试的数学成绩x、物理成绩y进行分析.下面是该生7次考试的成绩.
(Ⅰ)他的数学成绩与物理成绩哪个更稳定?请给出你的说明;
(Ⅱ)已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程
(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
| 数学 | 108 | 103 | 137 | 112 | 128 | 120 | 132 |
| 物理 | 74 | 71 | 88 | 76 | 84 | 81 | 86 |
(Ⅱ)已知该生的物理成绩y与数学成绩x是线性相关的,求物理成绩y与数学成绩x的回归直线方程
(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
 如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
如图,A1,A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS,OT围成一个平行四边形OPQR,则|OS|2+|OT|2=( ) 如图,在平面直角坐标系xOy中,椭圆Ω:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=2上的点和椭圆Ω上的点的距离的最小值为1.
如图,在平面直角坐标系xOy中,椭圆Ω:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\;(a>b>0)$的离心率为$\frac{{\sqrt{2}}}{2}$,直线l:y=2上的点和椭圆Ω上的点的距离的最小值为1. 我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积总相等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底长为1、下底长为2的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图1和图2所截得的两线段长总相等,则图1的面积为( )
我国南北朝时代的数学家祖暅提出体积的计算原理(组暅原理):“幂势既同,则积不容异”.“势”即是高,“幂”是面积.意思是:如果两等高的几何体在同高处截得两几何体的截面积总相等,那么这两个几何体的体积相等,类比祖暅原理,如图所示,在平面直角坐标系中,图1是一个形状不规则的封闭图形,图2是一个上底长为1、下底长为2的梯形,且当实数t取[0,3]上的任意值时,直线y=t被图1和图2所截得的两线段长总相等,则图1的面积为( )