题目内容
已知直线l1的斜率为-
,直线l2经过点M(1,1),N(0,-
),则两条直线的位置关系为( )
| 2 |
| 3 |
| 1 |
| 2 |
| A、平行 | B、相交但不垂直 |
| C、相交且垂直 | D、以上都不正确 |
考点:直线的斜率
专题:计算题,直线与圆
分析:求出直线l2的斜率,判断两条直线的位置关系,即可得到选项.
解答:
解:直线l2经过点M(1,1),N(0,-
),
∴直线l2的斜率为:
=
.
又直线l1的斜率为-
,
∵-
×
=-1,
∴两条直线垂直.
故选:C.
| 1 |
| 2 |
∴直线l2的斜率为:
1+
| ||
| 1-0 |
| 3 |
| 2 |
又直线l1的斜率为-
| 2 |
| 3 |
∵-
| 2 |
| 3 |
| 3 |
| 2 |
∴两条直线垂直.
故选:C.
点评:本题考查直线的斜率的求法,两条直线的位置关系,基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=(sinx+cosx)2的最小正周期为( )
| A、2π | ||
| B、π | ||
C、
| ||
D、
|
集合A={0,1,2,3,4},B={x|x2-x>0},则A∩B=( )
| A、{2,3,4} |
| B、{1} |
| C、{x|2<x≤4} |
| D、{x|x<0或x>2} |
已知函数f(x)=x3+(b-|a|)x2+(a2-4b)x是奇函数,则f′(0)的最小值是( )
| A、-4 | B、0 | C、1 | D、4 |
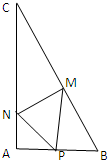 在Rt△ABC中,AB=2,AC=4,∠A为直角,P为AB中点,M、N分别是BC,AC上任一点,则△MNP周长的最小值是
在Rt△ABC中,AB=2,AC=4,∠A为直角,P为AB中点,M、N分别是BC,AC上任一点,则△MNP周长的最小值是