题目内容
设函数y=x2-3×2n-1x+2×4n-1（n∈N*）的图象在x轴上截得的抛物线长为dn，记数列{dn}的前n项和为Sn，若存在正整数n，使得log2（Sn+1） m-n2≥18成立，则实数m的最小值为 ．
考点：数列与解析几何的综合
专题：函数的性质及应用,等差数列与等比数列
分析：得出dn=2n-2n-1=2n-1，求出Sn，化简得出n（m-n2）≥18，构造函数g（n）=n2+
，运用导数判断即可得出m的最小值．
| 18 |
| n |
解答：
解：∵函数y=x2-3×2n-1x+2×4n-1（n∈N*）的图象在x轴上截得的抛物线长为dn=x2-x1，
得出dn=2n-2n-1=2n-1，
∵x2-3×2n-1x+2×4n-1=0（n∈N*），x1=2n-1，x2=2n，∴
=
=2，
∴{dn}为等比数列，d1=1，Sn=2n-1，
∴Sn+1=2n，
∵log2（Sn+1） m-n2≥18
∴n（m-n2）≥18存在正整数n，不等式成立．m≥n2+
g′（n）=2n-
=0，n=
g′（n）＞0，n＞
，
g′（n）＜0，n＜
，
g（n）=n2+
在（0，
）递减，在（
，+∞）
当n=1时，m≥19，
当n=2时，m≥13，
当n=3时，m≥15，
当n=4时，m≥16+
可知：实数m的最小值为13．
得出dn=2n-2n-1=2n-1，
∵x2-3×2n-1x+2×4n-1=0（n∈N*），x1=2n-1，x2=2n，∴
| dn+1 |
| dn |
| 2n |
| 2n-1 |
∴{dn}为等比数列，d1=1，Sn=2n-1，
∴Sn+1=2n，
∵log2（Sn+1） m-n2≥18
∴n（m-n2）≥18存在正整数n，不等式成立．m≥n2+
| 18 |
| n |
g′（n）=2n-
| 18 |
| n2 |
| 3 | 9 |
g′（n）＞0，n＞
| 3 | 9 |
g′（n）＜0，n＜
| 3 | 9 |
g（n）=n2+
| 18 |
| n |
| 3 | 9 |
| 3 | 9 |
当n=1时，m≥19，
当n=2时，m≥13，
当n=3时，m≥15，
当n=4时，m≥16+
| 9 |
| 2 |
可知：实数m的最小值为13．
点评：本题中考察了数列，函数，不等式，导数的运用相结合的题目，难度较大．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
sin（-660°）=（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
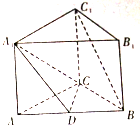如图，直三棱柱ABC-A
已知在平面直角坐标系中，坐标原点为O，点A，B在x轴上，OA=1，OB=5，点C在y轴上，OC=2.5，第一象限有一点D的坐标为（3，4），连接AD，BD，点E是线段AB上一动点（不与点A重合），过E作EF⊥AB交射线AD于点F，以EF为一边在EF的右侧作正方形EFGH，设E点的坐标为（t，0）