题目内容
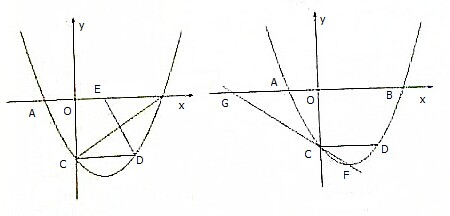
如图,已知开口向上的抛物线与x轴分别交于点A(m,0)和B(-3m,0)(其中m<0),与y轴交于点C(0,-3).点D在该抛物线上,CD∥AB.
(1)当m=-1时,求该抛物线所表示的函数关系式;
(2)在线段AB上是否存在点E,使得线段ED、BC互相垂直平分?若存在,求出点E的坐标,若不存在,请说明理由;
(3)设抛物线的顶点为F,作直线CF交x轴于点G,求证:
=
.

(1)当m=-1时,求该抛物线所表示的函数关系式;
(2)在线段AB上是否存在点E,使得线段ED、BC互相垂直平分?若存在,求出点E的坐标,若不存在,请说明理由;
(3)设抛物线的顶点为F,作直线CF交x轴于点G,求证:
| FC |
| CG |
| CD |
| GB |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线的定义、性质与方程
分析:(1)设出函数的表达式,代入C(0,-3),m=-1,求出即可;
(2)转化为证明四边形ECDB是菱形,根据菱形的定义判断即可;
(3)求出抛物线顶点坐标,从而求出直线FC的方程,解出G点坐标,从而求出比值.
(2)转化为证明四边形ECDB是菱形,根据菱形的定义判断即可;
(3)求出抛物线顶点坐标,从而求出直线FC的方程,解出G点坐标,从而求出比值.
解答:
解:(1)设函数为 y=a(x-m)(x+3m),(m<0)
∵函数经过C(0,-3),带入解析式得:-3=-3am2
∵m=-1,∴a=1
∴函数式y=(x+1)(x-3)=x2-2x-3=(x-1)2-4.
(2)由(1)可得 A(-1,0)B(3,0)
当y=-3时,x=2或x=0,
∵C(0,-3),
∴D(2,-3)
如果要求ED,CB垂直平分,则就是ECDB为菱形.
就是要在x轴上找到E,使得EC∥DB,且EC=CD
可求出CD=2,BD=
,
∴以C,D,B,E为顶点的四边形是不可能构成菱形的,
所以不可能存在点E满足题意;
(3)由(1)得,抛物线的顶点F(1,-4),
又C(0,-3),所以CF直线解析式为:y=-x-3.
∴G(-3,0)
CF=
,CG=3
,CD=2,GB=6.
∴
=
=3.
∵函数经过C(0,-3),带入解析式得:-3=-3am2
∵m=-1,∴a=1
∴函数式y=(x+1)(x-3)=x2-2x-3=(x-1)2-4.
(2)由(1)可得 A(-1,0)B(3,0)
当y=-3时,x=2或x=0,
∵C(0,-3),
∴D(2,-3)
如果要求ED,CB垂直平分,则就是ECDB为菱形.
就是要在x轴上找到E,使得EC∥DB,且EC=CD
可求出CD=2,BD=
| 10 |
∴以C,D,B,E为顶点的四边形是不可能构成菱形的,
所以不可能存在点E满足题意;
(3)由(1)得,抛物线的顶点F(1,-4),
又C(0,-3),所以CF直线解析式为:y=-x-3.
∴G(-3,0)
CF=
| 2 |
| 2 |
∴
| FC |
| GC |
| CD |
| GB |
点评:本题考查了求抛物线的解析式问题,考查了菱形的判定,考查了线段成比例问题,是一道综合题.

练习册系列答案
相关题目
已知等比数列{an}满足log3a4=log3a3-1,且s3=9,则log
(a1+a5+a6)的值是( )
| 1 |
| 3 |
| A、-1 | B、-2 | C、2 | D、1 |
已知定义在(-1,1)上的函数f(x)=x-sinx,若f(a-2)+f(4-a2)<0,则a的取值范围是( )
A、(2,
| ||||
B、(
| ||||
| C、(0,2) | ||||
| D、(-∞,-1)∪(2,+∞) |
在△ABC中,a=x,b=2,B=45°,若该三角形有两个解,则x的取值范围是( )
| A、x>2 | ||
| B、x<2 | ||
C、2
| ||
D、2
|