题目内容
已知等差数列{an}满足:a2=5,a4+a6=22,{an}的前n项和为Sn.
(1)求an及Sn;
(2)若f(x)=
,bn=f(an)(n∈N*),求数列{bn}的前n项和Sn.
(1)求an及Sn;
(2)若f(x)=
| 1 |
| x2-1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)设等差数列{an}的首项为a1,公差为d,由已知可解得a1,d的值,从而可求an及Sn;
(2)由(1)及已知可求得bn=
=
(
-
),从而可求数列{bn}的前n项和Sn.
(2)由(1)及已知可求得bn=
| 1 |
| 4n(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
解答:
解:(1)设等差数列{an}的首项为a1,公差为d
∵a2=5,a4+a6=22,
∴a1+d=5,2a1+8d=22,
解得a1=3,d=2,
∴an=2n+1,Sn=n2+2n.
(2)∵f(x)=
,bn=f(an),
∴bn=
,
∵an=2n+1∴an2-1=4n(n+1),
∴bn=
=
(
-
),
Sn=b1+b2+…+bn=
(1-
+
-
+…+
-
)=
(1-
)=
.
所以数列{bn}的前n项和Sn=
.
∵a2=5,a4+a6=22,
∴a1+d=5,2a1+8d=22,
解得a1=3,d=2,
∴an=2n+1,Sn=n2+2n.
(2)∵f(x)=
| 1 |
| x2-1 |
∴bn=
| 1 |
| an2-1 |
∵an=2n+1∴an2-1=4n(n+1),
∴bn=
| 1 |
| 4n(n+1) |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+1 |
Sn=b1+b2+…+bn=
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 4 |
| 1 |
| n+1 |
| n |
| 4(n+1) |
所以数列{bn}的前n项和Sn=
| n |
| 4(n+1) |
点评:本题主要考察了等差数列的通项公式和求和公式的应用,属于基础题.

练习册系列答案
相关题目
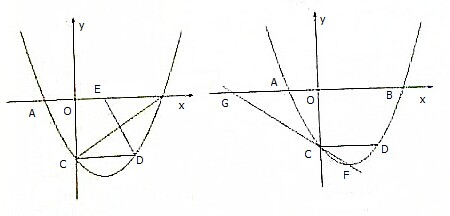
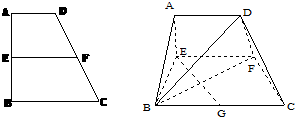 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=