题目内容
已知等比数列{an}满足log3a4=log3a3-1,且s3=9,则log
(a1+a5+a6)的值是( )
| 1 |
| 3 |
| A、-1 | B、-2 | C、2 | D、1 |
考点:等比数列的通项公式
专题:计算题,等差数列与等比数列
分析:运用对数的运算法则,可得等比数列{an}的公比q为
,再由等比数列的通项公式,即得log
(a4+a5+a6)=log
q3(a1+a2+a3),再由条件和对数的运算性质,即可得到答案.
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:
解:log3a4=log3a3-1
即有log3a4-log3a3=-1,
则log3
=-1,
即
=
,即等比数列{an}的公比q为
,
则log
(a4+a5+a6)=log
q3(a1+a2+a3)
=log
(
)3×9=log
=1,
故选D.
即有log3a4-log3a3=-1,
则log3
| a4 |
| a3 |
即
| a4 |
| a3 |
| 1 |
| 3 |
| 1 |
| 3 |
则log
| 1 |
| 3 |
| 1 |
| 3 |
=log
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
故选D.
点评:本题考查等比数列的通项公式及运用,考查对数的运算法则及求值,考查运算能力,属于中档题.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
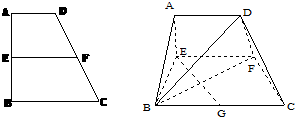 已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=
已知梯形ABCD中,AD∥BC,∠ABC=∠BAD=