题目内容
设集合A={(x,y)|
≤(x-2)2+y2≤m2,x,y∈R},B={(x,y)|2m≤x+y≤2m+1,x,y∈R},若A∩B=∅,则实数m的取值范围是( )
| m |
| 2 |
A、
| ||||
B、0<m<2+
| ||||
C、m<2-
| ||||
D、m<
|
考点:交集及其运算
专题:集合
分析:首先求出A∩B≠∅时m的范围,方法为:由集合B得到其表示的点集,然后对是否为空集分类,当A不是空集时,再由m≤0或m≥
时分类,若m≤0,则A={(x,y)|(x-2)2+y2≤m2,x,y∈R}表示以点(2,0)为圆心,半径为|m|的圆面(m=0时是点(2,0)),由点(2,0)到直线x+y=2m+1的距离不大于半径|m|求解m的范围;若m≥
,则A={(x,y)|
≤(x-2)2+y2≤m2,x,y∈R}表示以点(2,0)为圆心,大圆半径为|m|,小圆半径为
的圆环.然后再把m由1分界,m小于等于1时显然成立,m>1时再由点(2,0)到直线x+y=2m的距离不大于半径|m|列式求解m的范围,即可确定出A∩N=∅时m的范围.
| 1 |
| 2 |
| 1 |
| 2 |
| m |
| 2 |
| ||
|
解答:
解:∵对任意m∈R,都有2m≤2m+1,所以B≠∅,
集合B表示在直线x+y=2m与直线x+y=2m+1之间的平面区域(包含边界).
当
>m2,即0<m<
时,A=∅,不满足条件;
当
≤m2,即m≤0或m≥
时,A≠∅.
(1)若m≤0,则A={(x,y)|(x-2)2+y2≤m2,x,y∈R}表示以点(2,0)为圆心,
半径为|m|的圆面(m=0时是原点),
A∩B≠∅等价于点(2,0)到直线x+y=2m+1的距离不大于半径|m|,
即
≤|m|,即2m2-4m+1≤0,即(m-1)2≤
,解得1-
≤m≤1+
,所以m∈∅;
(2)若m≥
,则A={(x,y)|
≤(x-2)2+y2≤m2,x,y∈R}表示以点(2,0)为圆心,
大圆半径为|m|,小圆半径为
的圆环.
当(2,0)∈B,即2m≤2≤2m+1,即
≤m≤1时,A∩B≠∅,满足条件;
若m>1,则A∩B≠∅等价于点(2,0)到直线x+y=2m的距离不大于半径|m|,
即
≤|m|,即m2-4m+2≤0,即(m-2)2≤2,解得2-
≤m≤2+
,所以1<m≤2+
,满足条件.
综上,A∩B≠∅时,实数m的取值范围是[
,2+
],
则A∩B=∅,则实数m的取值范围是m<
或m>2+
.
故选:D.
集合B表示在直线x+y=2m与直线x+y=2m+1之间的平面区域(包含边界).
当
| m |
| 2 |
| 1 |
| 2 |
当
| m |
| 2 |
| 1 |
| 2 |
(1)若m≤0,则A={(x,y)|(x-2)2+y2≤m2,x,y∈R}表示以点(2,0)为圆心,
半径为|m|的圆面(m=0时是原点),
A∩B≠∅等价于点(2,0)到直线x+y=2m+1的距离不大于半径|m|,
即
| |2-2m-1| | ||
|
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
(2)若m≥
| 1 |
| 2 |
| m |
| 2 |
大圆半径为|m|,小圆半径为
| ||
|
当(2,0)∈B,即2m≤2≤2m+1,即
| 1 |
| 2 |
若m>1,则A∩B≠∅等价于点(2,0)到直线x+y=2m的距离不大于半径|m|,
即
| |2-2m| | ||
|
| 2 |
| 2 |
| 2 |
综上,A∩B≠∅时,实数m的取值范围是[
| 1 |
| 2 |
| 2 |
则A∩B=∅,则实数m的取值范围是m<
| 1 |
| 2 |
| 2 |
故选:D.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知a=log23+log2
,b=log23
,c=log32,则a,b,c的大小关系是( )
| 3 |
| 3 |
| A、a=b>c |
| B、a=b<c |
| C、a<b<c |
| D、a>b>c |
直线a,b异面,a∥平面α,则对于下列论断正确的是( )
①一定存在平面α使b⊥α;
②一定存在平面α使b∥α;
③一定存在平面α使b⊆α;
④一定存在无数个平面α与b交于一定点.
①一定存在平面α使b⊥α;
②一定存在平面α使b∥α;
③一定存在平面α使b⊆α;
④一定存在无数个平面α与b交于一定点.
| A、①④ | B、②③ |
| C、①②③ | D、②③④ |
下边程序运行后的输出结果为( )


| A、17 | B、19 | C、21 | D、23 |
已知f(x)=cosx,则f′(
)=( )
| π |
| 2 |
| A、1 | B、0 | C、-1 | D、2 |
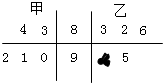 如图茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损.则甲的平均成绩超过乙的平均成绩的概率为( )
如图茎叶图表示的是甲、乙两人在5次综合测评中的成绩,其中一个数字被污损.则甲的平均成绩超过乙的平均成绩的概率为( )A、
| ||
B、
| ||
C、
| ||
D、
|
直线l过点P(1,2)且倾斜角是直线x-2y=0倾斜角的2倍,则直线l的方程是( )
| A、3x-4y+5=0 |
| B、x-y=0 |
| C、4x-3y+2=0 |
| D、2x-y=0 |
已知以原点O为圆心的单位圆上有一质点P,它从初始位置P0(
,
)开始,按逆时针方向以角速度1rad/s做圆周运动.则点P的纵坐标y关于时间t的函数关系为( )
| 1 |
| 2 |
| ||
| 2 |
A、y=sin(t+
| ||
B、y=sin(t+
| ||
C、y=cos(t+
| ||
D、y=cos(t+
|