题目内容
已知△ABC的内角A，B，C所对的边分别为a，b，c，若c2＜a2+b2+2abcos2C，则∠C的可能取值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：余弦定理
专题：解三角形
分析：利用余弦定理和已知不等式可求得关于cosC的一元二次不等式，进而求得cosC的范围，则C的范围可得，对四个选项验证即可．
解答：
解：∵c2＜a2+b2+2abcos2C，
∴cos2C＞-
=-cosc，
∴2cos2C-1+cosC＞0，
∴cosC＞
或cos＜-1（舍去），
∴0＜C＜
，
∴只有D项符合．
故选D．
∴cos2C＞-
| a2+b2-c2 |
| 2ab |
∴2cos2C-1+cosC＞0，
∴cosC＞
| 1 |
| 2 |
∴0＜C＜
| π |
| 3 |
∴只有D项符合．
故选D．
点评：本题主要考查了余弦定理的应用．解题过程中结合了二倍角公式和一元二次不等式的相干知识，综合性较强．
练习册系列答案
相关题目
把函数f（x）=sin（2x-
）的图象向左平移φ（0＜φ＜π）个单位可以得到函数g（x）的图象，若g（x）的图象关于y轴对称，则φ的值为（ ）
| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
下边程序运行后的输出结果为（ ）
| A、17 | B、19 | C、21 | D、23 |
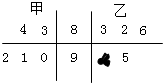如图茎叶图表示的是甲、乙两人在5次综合测评中的成绩，其中一个数字被污损．则甲的平均成绩超过乙的平均成绩的概率为（ ）A、
| ||
B、
| ||
C、
| ||
D、
|
直线l过点P（1，2）且倾斜角是直线x-2y=0倾斜角的2倍，则直线l的方程是（ ）
| A、3x-4y+5=0 |
| B、x-y=0 |
| C、4x-3y+2=0 |
| D、2x-y=0 |
设全集U=Z，A={-1，0，1，2}，B{x|x2-2x=0}，则A∩∁UB为（ ）
| A、{2} |
| B、{-1，0，1} |
| C、{0，2} |
| D、{-1，1} |
已知以原点O为圆心的单位圆上有一质点P，它从初始位置P0（
，
）开始，按逆时针方向以角速度1rad/s做圆周运动．则点P的纵坐标y关于时间t的函数关系为（ ）
| 1 |
| 2 |
| ||
| 2 |
A、y=sin（t+
| ||
B、y=sin（t+
| ||
C、y=cos（t+
| ||
D、y=cos（t+
|