题目内容
2．在△ABC中，角A，B，C的对边分别为a，b，c，且满足$\frac{2a-b}{cosB}=\frac{c}{cosC}$．（1）求角C的值；
（2）若c=7，△ABC的面积为$10\sqrt{3}$，求a+b的值．
分析 （1）已知等式利用正弦定理化简，整理后利用两角和与差的正弦函数公式及诱导公式化简，求出cosC的值，即可确定出C的度数；
（2）利用三角形面积公式列出关系式，把已知面积与sinC的值代入求出ab的值，再利用余弦定理列出关系式，整理即可求出a+b的值．
解答 解：（1）已知等式利用正弦定理化为$\frac{2sinA-sinB}{cosB}$=$\frac{sinC}{cosC}$，
整理得：2sinAcosC=sinBcosC+sinCcosB=sin（B+C）=sinA，
∵0＜A＜π，∴sinA≠0，
∴cosC=$\frac{1}{2}$，
又∵0＜C＜π，∴C=$\frac{π}{3}$；
（2）由S△ABC=$\frac{1}{2}$absinC=$\frac{1}{2}$absin$\frac{π}{3}$=10$\sqrt{3}$，得ab=40，
∵cosC=$\frac{1}{2}$，
∴由余弦定理得：c2=a2+b2-2abcosC=（a+b）2-3ab=（a+b）2-3×40，
∴49=（a+b）2-3×40，即（a+b）2=169，
开方得：a+b=13．
点评 此题考查了正弦、余弦定理，三角形面积公式，熟练掌握定理及公式是解本题的关键．
练习册系列答案
相关题目
12．已知直线l1的方程为Ax+3y+C=0，直线l2的方程为2x-3y+4=0，若l1与l2的交点在y轴上，则C的值为（ ）
| A． | 4 | B． | -4 | C． | ±4 | D． | 与A有关 |
13．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的焦点的渐近线的距离为2，且双曲线的一条渐近线与直线x-2y+3=0平行，则双曲线的方程为（ ）
| A． | $\frac{x^2}{16}-\frac{y^2}{4}=1$ | B． | $\frac{x^2}{9}-\frac{y^2}{4}=1$ | C． | $\frac{x^2}{4}-\frac{y^2}{9}=1$ | D． | $\frac{x^2}{8}-\frac{y^2}{4}=1$ |
10．已知某几何体的三视图如图，则该几何体的体积是（ ）
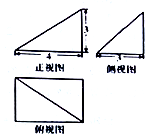
| A． | 48 | B． | 36 | C． | 24 | D． | 12 |
7．已知命题p：?x∈R，$sinx＞\frac{{\sqrt{3}}}{2}$，则（ ）
| A． | ﹁p：?x∈R，sin $x≤\frac{{\sqrt{3}}}{2}$ | B． | ﹁p：?x∈R，$sinx＜\frac{{\sqrt{3}}}{2}$ | ||
| C． | ﹁p：?x∈R | D． | ﹁p：?x∈R，$sinx≤\frac{{\sqrt{3}}}{2}$ |
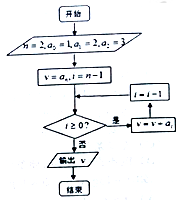
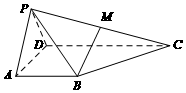在四棱锥P-ABCD中，平面PAD⊥平面ABCD，△PAD为等边三角形，$AB=AD=\frac{1}{2}CD$，AB⊥AD，AB∥CD，点M是PC的中点．
11．a＞b的一个充分不必要条件是（ ）
| A． | a=1，b=0 | B． | $\frac{1}{a}$＜$\frac{1}{b}$ | C． | a2＞b2 | D． | a3＞b3 |