题目内容
7.数列{an}满足a1=2,an+1=$\frac{2(n+2)}{n+1}$an(n∈N*),$\frac{{a}_{2017}}{{a}_{1}+{a}_{2}+…+{a}_{2016}}$=( )| A. | $\frac{1009}{1008}$ | B. | $\frac{2015}{1007}$ | C. | $\frac{2016}{2015}$ | D. | $\frac{2015}{2014}$ |
分析 利用$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{2(n+2)}{n+1}$及a1=2累乘可知an=(n+1)2n-1,进而利用错位相减法计算可知Sn=n•2n,代入计算即得结论.
解答 解:因为an+1=$\frac{2(n+2)}{n+1}$an(n∈N*),
所以$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{2(n+2)}{n+1}$,
又因为a1=2,
所以当n≥2时,$\frac{{a}_{n}}{{a}_{1}}$=$\frac{{a}_{n}}{{a}_{n-1}}$•$\frac{{a}_{n-1}}{{a}_{n-2}}$•…•$\frac{{a}_{2}}{{a}_{1}}$
=$\frac{2(n+1)}{n}$•$\frac{2n}{n-1}$•…•$\frac{2×(1+2)}{1+1}$
=$\frac{n+1}{2}$•2n-1,
所以an=2•$\frac{n+1}{2}$•2n-1=(n+1)2n-1,
记数列{an}的前n项和为Sn,
则Sn=2×20+3×21+…+(n+1)2n-1,
2Sn=2×21+3×22+…+(n+1)2n,
两式相减,得:-Sn=2+(21+22+…+2n-1)-(n+1)2n=2+$\frac{2(1-{2}^{n-1})}{1-2}$-(n+1)2n,
所以Sn=n•2n,
所以$\frac{{a}_{2017}}{{a}_{1}+{a}_{2}+…+{a}_{2016}}$=$\frac{2018•{2}^{2016}}{2016•{2}^{2016}}$=$\frac{1009}{1008}$,
故选:A.
点评 本题考查数列的通项及前n项和,考查累加法求通项,考查错位相减法求和,考查运算求解能力,注意解题方法的积累,属于中档题.

| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{3}$ |
| A. | -6 | B. | 13 | C. | $\frac{3}{2}$ | D. | $\sqrt{13}$ |
| A. | 在(0,+∞)内是增函数 | B. | 在(1,+∞)内是增函数 | ||
| C. | 在(-∞,0)内是增函数 | D. | 在(-∞,1)内是增函数 |
| A. | y=tan3x | B. | y=cos2x+1 | C. | y=2sinx-1 | D. | y=2x |
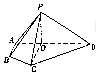 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,O为为AD上的一点,且AB⊥AD,CO⊥AD,AB=AO=$\frac{1}{3}$AD=$\frac{1}{2}$OC=1,OP=$\frac{1}{2}$CD,PA=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,O为为AD上的一点,且AB⊥AD,CO⊥AD,AB=AO=$\frac{1}{3}$AD=$\frac{1}{2}$OC=1,OP=$\frac{1}{2}$CD,PA=$\sqrt{3}$.