题目内容
10.已知函数f(x)=x2-1-2alnx(a≠0),求函数f(x)的极值.分析 求函数的定义域和导数,分类讨论,利用函数单调性和极值与导数之间的关系即可得到结论.
解答 解:∵f(x)=x2-1-2alnx(a≠0)∴f(x)的定义域为{x|x>0},且$f'(x)=2x-\frac{2a}{x}=\frac{{2({x^2}-a)}}{x}$
(1)当a<0时,∵x>0,且x2-a>0,
∴f'(x)>0对x>0恒成立,
∴f(x)在(0,+∞)上单调递增,f(x)无极值.
(2)当a>0时
令f'(x)=0,即x2-a=0,解得$x=\sqrt{a}$或$x=-\sqrt{a}$(舍去)
当x变化时,f'(x),f(x)的变化情况如下表:
| x | $(0,\sqrt{a})$ | $\sqrt{a}$ | $(\sqrt{a},+∞)$ |
| f'(x) | - | 0 | + |
| f(x) | ↘ | 极小值 | ↗ |
综上,当a<0时,函数f(x)在(0,+∞)上无极值;当a>0时,f(x)在$x=\sqrt{a}$处取得极小值a-1-alna.
点评 本题主要考查函数单调性和极值,考查导数与函数单调性及极值的关系,考查分类讨论思想,属于中档题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
1.如图的程序框图,其作用是输入x的值,输出相应的y值,若x=y,则这样的x值有( )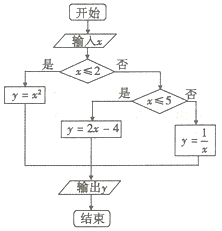

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.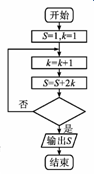 某程序框图如图所示,若输出的S=29,则判断框内应填( )
某程序框图如图所示,若输出的S=29,则判断框内应填( )
 某程序框图如图所示,若输出的S=29,则判断框内应填( )
某程序框图如图所示,若输出的S=29,则判断框内应填( )| A. | k>5? | B. | k>4? | C. | k>7? | D. | k>6? |
15.已知函数f(x)=$\frac{{lnx+{{(x-b)}^2}}}{x}$,若存在x∈[$\frac{1}{2}$,2],使得xf'(x)+f(x)>0,则实数b的取值范围是( )
| A. | $(-∞,\frac{3}{2})$ | B. | $(-∞,\frac{3}{2}]$ | C. | $(-∞,\frac{9}{4})$ | D. | $(-∞,\frac{9}{4}]$ |
20.已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,学校决定利用随机数表法从中抽取100人进行成绩抽样调查.抽取的100人的数学与地理的水平测试成绩如下表:
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人.
(1)在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩及格的学生中,已知a≥10,b≥7,求数学成绩优秀的人数比及格的人数少的概率.
| 人数 | 数学 | |||
| 优秀 | 良好 | 及格 | ||
| 地理 | 优秀 | 7 | 20 | 5 |
| 良好 | 9 | 18 | 6 | |
| 及格 | a | 4 | b | |
(1)在该样本中,数学成绩优秀率是30%,求a,b的值;
(2)在地理成绩及格的学生中,已知a≥10,b≥7,求数学成绩优秀的人数比及格的人数少的概率.
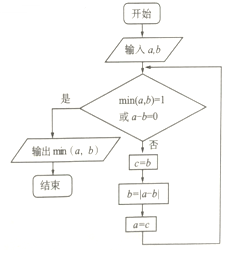 min(a,b)表示中的最小值.执行如图所示的程序框图,若输入的a,b值分别为6,4,则输出的min(a,b)值是( )
min(a,b)表示中的最小值.执行如图所示的程序框图,若输入的a,b值分别为6,4,则输出的min(a,b)值是( )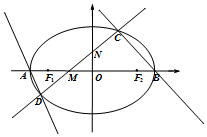 如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,
如图,椭圆E的左右顶点分别为A、B,左右焦点分别为F1、F2,$|{AB}|=4,|{{F_1}{F_2}}|=2\sqrt{3}$,