题目内容
7.设i是虚数单位,若$\frac{z}{i}$=$\frac{i-3}{1+i}$,则复数$\overline{z}$的虚部为( )| A. | 1 | B. | 2 | C. | -1 | D. | -2 |
分析 把已知等式变形,再利用复数代数形式的乘除运算化简复数z,求出$\overline{z}$得答案.
解答 解:由$\frac{z}{i}$=$\frac{i-3}{1+i}$,
得$z=\frac{i(i-3)}{1+i}=\frac{-1-3i}{1+i}=\frac{(-1-3i)(1-i)}{(1+i)(1-i)}$=$\frac{-4-2i}{2}=-2-i$,
∴$\overline{z}=-2+i$.
∴复数$\overline{z}$的虚部为:1.
故选:A.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.设集合U={-2,-1,0,1,2},A={x|x2-x-2=0},则∁UA=( )
| A. | {-2,1} | B. | {-1,2} | C. | {-2,0,1} | D. | {2,-1,0} |
12.图,网格纸上小正方形的边长为1,粗线画出的是某个四面体的三视图,则该四面体的体积为( )

| A. | 16 | B. | $\frac{4}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{8}{3}$ |
19.设集合A={x|x<0},B={x|x2≤1},则A∩B等于( )
| A. | (-1,0) | B. | [-1,0) | C. | (-∞,-1] | D. | (-∞,-1) |
13.函数f(x)=aex-2-lnx+1的图象在点(2,f(2))处的切线斜率为$\frac{5}{2}$,则实数a=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
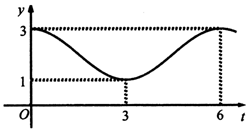 某工厂有甲、乙两生产车间,其污水瞬时排放量y(单位:m3/h )关于时间t(单位:h)的关系均近似地满足函数y=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π),其图象如下:
某工厂有甲、乙两生产车间,其污水瞬时排放量y(单位:m3/h )关于时间t(单位:h)的关系均近似地满足函数y=Asin(ωt+φ)+b(A>0,ω>0,0<φ<π),其图象如下: