题目内容
20.已知函数f(x)=x2+bx+c满足f(1-x)=f(1+x),f(0)>0,且f(m)=f(n)=0(m≠n),则${log_3}m-{log_{\frac{1}{3}}}n$的值( )| A. | 大于0 | B. | 等于0 | C. | 小于0 | D. | 无法确定 |
分析 利用二次函数的性质求出对称轴方程,推出m+n的值,然后求解表达式的值即可.
解答 解:函数f(x)=x2+bx+c满足f(1-x)=f(1+x),可得函数的对称轴为:x=1,
f(0)>0,且f(m)=f(n)=0(m≠n),
可得m+n=2,m>0,n>0.
mn<$(\frac{m+n}{2})^{2}$=1.
则${log_3}m-{log_{\frac{1}{3}}}n$=log3m+log3n=log3(mn)<0.
故选:C.
点评 本题考查二次函数的性质,基本不等式在最值中的应用,考查计算能力.

练习册系列答案
相关题目
10.若sinα+sinβ+sinγ=0,cosα+cosβ+cosγ=0,且0≤α<β<γ<2π,则β-α=( )
| A. | $\frac{4π}{3}或\frac{2π}{3}$ | B. | $\frac{2π}{3}$ | C. | $\frac{4π}{3}$ | D. | 以上答案都不对 |
5.如图,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$-$\overrightarrow{b}$=( )
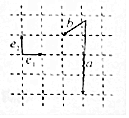

| A. | 3$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$ | B. | -2$\overrightarrow{{e}_{1}}$-4$\overrightarrow{{e}_{2}}$ | C. | $\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$ | D. | 3$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$ |
12.设由不等式组$\left\{\begin{array}{l}{x-y+2≥0}\\{y+2≥0}\\{x+y+2≤0}\end{array}\right.$表示的平面区域为Ω,P∈Ω,过点P作圆O:x2+y2=1的两条切线,切点分别为A、B,记∠APB=α,则当α最小时,cosα=( )
| A. | $\frac{\sqrt{95}}{10}$ | B. | $\frac{19}{20}$ | C. | $\frac{9}{10}$ | D. | $\frac{1}{2}$ |
10.某高校通过调查在发现该校毕业生的学习成绩与就业情况具有线性相关关系,现对5名毕业生的数据进行分析,他们的专业课成绩xi及现在的工作年薪yi情况如下:
(1)根据表中数据,计算专业课成绩与年薪的线性相关系数;
(2)求出专业课成绩与年薪关系的线性回归方程,并预测专业课成绩为9.6分的学生毕业后的年薪;
(3)若再从这5名毕业生中随机抽取2名进行详细调查,求恰有一名毕业生的专业课成绩不少于9分的概率.附:r=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sqrt{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}•\sqrt{\sum_{i=1}^{n}{y}_{i}^{2}-n{\overline{y}}^{2}}}$,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.
| 专业课成绩xi(分) | 7 | 7 | 8 | 9 | 9 |
| 年薪yi(万元) | 10 | 12 | 14 | 14 | 15 |
(2)求出专业课成绩与年薪关系的线性回归方程,并预测专业课成绩为9.6分的学生毕业后的年薪;
(3)若再从这5名毕业生中随机抽取2名进行详细调查,求恰有一名毕业生的专业课成绩不少于9分的概率.附:r=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sqrt{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}•\sqrt{\sum_{i=1}^{n}{y}_{i}^{2}-n{\overline{y}}^{2}}}$,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$.