题目内容
5.如图,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$-$\overrightarrow{b}$=( )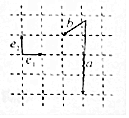
| A. | 3$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$ | B. | -2$\overrightarrow{{e}_{1}}$-4$\overrightarrow{{e}_{2}}$ | C. | $\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$ | D. | 3$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$ |
分析 根据两个向量的加减法的法则,以及其几何意义即可求出
解答 解:设向量$\overrightarrow{a}$的终点为A,向量$\overrightarrow{b}$的终点为B,则$\overrightarrow{BA}$=$\overrightarrow{a}$-$\overrightarrow{b}$,
而$\overrightarrow{BA}$=$\overrightarrow{{e}_{{\;}_{1}}}$-3$\overrightarrow{{e}_{2}}$,
∴$\overrightarrow{a}$-$\overrightarrow{b}$=$\overrightarrow{{e}_{{\;}_{1}}}$-3$\overrightarrow{{e}_{2}}$,
故选:C
点评 本题主要考查平面向量基本定理的应用,两个向量的加减法的法则,以及其几何意义,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.化简式子$\frac{{tan({π+α})cos({2π-α})}}{{sin({\frac{3π}{2}+α})}}$的结果为( )
| A. | 1 | B. | -1 | C. | tanα | D. | -tanα |
16.直线x+2y+2=0与直线2x+y-2=0的交点坐标是( )
| A. | (2,-2) | B. | (-2,2) | C. | (-2,1) | D. | (3,-4) |
13.若变量x,y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤2}\\{y≥-1}\end{array}\right.$,则$\frac{y-2}{x-4}$的取值范围是( )
| A. | [0,3] | B. | [$\frac{1}{3}$,3] | C. | [$\frac{4}{3}$,4] | D. | [$\frac{1}{3}$,2] |
20.已知函数f(x)=x2+bx+c满足f(1-x)=f(1+x),f(0)>0,且f(m)=f(n)=0(m≠n),则${log_3}m-{log_{\frac{1}{3}}}n$的值( )
| A. | 大于0 | B. | 等于0 | C. | 小于0 | D. | 无法确定 |
10.设函数f(x)=sinx•cosx(x∈R),则函数f(x)在[0,π]上的单调递减区间为( )
| A. | [$\frac{π}{6}$,$\frac{π}{3}$] | B. | [$\frac{π}{6}$,$\frac{π}{2}$] | C. | [$\frac{π}{4}$,$\frac{3π}{4}$] | D. | [$\frac{3π}{4}$,π] |
 运行如图所示程序框图,若输入值x∈[-2,2],则输出值y的取值范围是[-1,6].
运行如图所示程序框图,若输入值x∈[-2,2],则输出值y的取值范围是[-1,6].