题目内容
4.点P(x,y)的坐标满足约束条件$\left\{\begin{array}{l}x-2y≥0\\ x+2y+4≥0\\ 7x+2y-8≤0\end{array}\right.$,由点P向圆C:(x+2)2+(y-1)2=1作切线PA,切点为A,则线段|PA|的最小值为( )| A. | $\frac{{4\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{55}}}{5}$ | C. | $\sqrt{19}$ | D. | $\frac{{\sqrt{33}}}{2}$ |
分析 画出不等式组$\left\{\begin{array}{l}x-2y≥0\\ x+2y+4≥0\\ 7x+2y-8≤0\end{array}\right.$表示的平面区域,根据题意过圆心C作直线x-2y=0的垂线,垂足为P,则线段|PA|的值即为所求.
解答 解:画出不等式组$\left\{\begin{array}{l}x-2y≥0\\ x+2y+4≥0\\ 7x+2y-8≤0\end{array}\right.$表示的平面区域为△ABC所围成的区域(包含边界):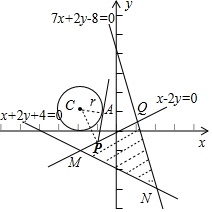
由点P向圆C:(x+2)2+(y-1)2=1作切线PA,
切点为A,连接AC,则|AC|=r=1;
过圆心C作直线x-2y=0的垂线,垂足为P,
则|PC|=$\frac{|-2-2×1|}{\sqrt{{1}^{2}{+(-2)}^{2}}}$=$\frac{4}{\sqrt{5}}$;
∴线段|PA|的最小值为
$\sqrt{{|PC|}^{2}{-r}^{2}}$=$\sqrt{{(\frac{4}{\sqrt{5}})}^{2}{-1}^{2}}$=$\frac{\sqrt{55}}{5}$.
故选:B.
点评 本题考查了线性规划的应用问题,也考查了数形结合的应用问题,是综合题.

练习册系列答案
相关题目
14.在等差数列{an}中,前n项和为Sn,且S2011=-2011,a1012=3,则S2017等于( )
| A. | 1009 | B. | -2017 | C. | 2017 | D. | -1009 |
15.在数字1、2、3、4中随机选两个数字,则选中的数字中至少有一个是偶数的概率为( )
| A. | $\frac{11}{12}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{6}$ | D. | $\frac{5}{8}$ |
12.已知Sn是数列{an}的前n项之和,a1=2,2Sn+1=Sn+4(n∈N*),则函数f(n)=Sn的值域是( )
| A. | (0,2] | B. | [2,4) | C. | [2,+∞) | D. | [2,3] |
9.sin40°sin10°+cos40°sin80°=( )
| A. | $\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | cos50° | D. | $\frac{{\sqrt{3}}}{2}$ |