题目内容
9. 已知f(x)=Asin (ω x+φ)+(A>0,ω>0,|φ|<π})的图象如图所示,则f(3π)=( )
已知f(x)=Asin (ω x+φ)+(A>0,ω>0,|φ|<π})的图象如图所示,则f(3π)=( )| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
分析 首先通过最高点与相邻零点横坐标得到函数的周期,通过图象经过的最高点得到A,和φ,然后求函数值.
解答 解:由函数图象得到函数的周期为T=4($\frac{9π}{4}-\frac{3π}{4}$)=6π=$\frac{2π}{ω}$,所以$ω=\frac{1}{3}$,
由图象经过最高点($\frac{3π}{4}$,2),所以A=2,并且sin($\frac{1}{3}×\frac{3π}{4}+$φ)=1,所以φ=$\frac{π}{4}$,
所以f(x)=2sin($\frac{1}{3}$x$+\frac{π}{4}$),所以f(3π)=2sin($π+\frac{π}{4}$)=$-\sqrt{2}$;
故选A.
点评 本题考查了三角函数的图象;注意相邻最高点与零点,得到周期、振幅以及初相;熟练掌握正弦函数的图象是关键.

练习册系列答案
相关题目
20.已知数列{an}的前n项和是Sn,则下列四个命题中,错误的是( )
| A. | 若数列{an}是公差为d的等差数列,则数列{$\frac{{S}_{n}}{n}$}的公差为$\frac{d}{2}$的等差数列 | |
| B. | 若数列{$\frac{{S}_{n}}{n}$}是公差为d的等差数列,则数列{an}是公差为2d的等差数列 | |
| C. | 若数列{an}是等差数列,则数列的奇数项,偶数项分别构成等差数列 | |
| D. | 若数列{an}的奇数项,偶数项分别构成公差相等的等差数列,则{an}是等差数列 |
4.已知$α∈(0,\frac{π}{2})$,且$2cos2α=cos(α-\frac{π}{4})$,则sin2α的值为( )
| A. | $\frac{1}{8}$ | B. | $-\frac{1}{8}$ | C. | $-\frac{7}{8}$ | D. | $\frac{7}{8}$ |
14.tan40°+tan80°-$\sqrt{3}$tan40°tan80°的值是( )
| A. | $\sqrt{3}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
18.二面角α-AB-β的平面角是锐角θ,M∈α,MN⊥β,N∈β,C∈AB,∠MCB为锐角,则( )
| A. | ∠MCN<θ | B. | ∠MCN=θ | ||
| C. | ∠MCN>θ | D. | 以上三种情况都有可能 |
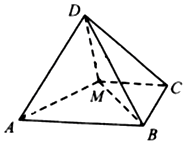 如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM.
如图,四棱锥D-ABCM中,AD⊥DM,底面四边形ABCM是直角梯形,AB⊥BC,MC⊥BC,且AB=2BC=2CM=4,平面AMD⊥平面ABCM. 如图,在△ABC中,D为BC的中点,E为AD的中点,直线BE与边AC交于点F,若AD=BC=6,则$\overrightarrow{AB}•\overrightarrow{CF}$=-18.
如图,在△ABC中,D为BC的中点,E为AD的中点,直线BE与边AC交于点F,若AD=BC=6,则$\overrightarrow{AB}•\overrightarrow{CF}$=-18.