题目内容
已知数列{an}是等差数列，若a1+a5=24，a4=8，则数列{an}的公差等于（ ）
| A、6 | B、-6 | C、4 | D、-4 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：由等差数列的性质，结合a1+a5=10求出a3，由等差数列的定义求得公差．
解答：
解：在等差数列{an}中，由a1+a5=24，得2a3=24，∴a3=12．
又a4=8，∴数列{an}的公差d为a4-a3=8-12=-4．
故选：D．
又a4=8，∴数列{an}的公差d为a4-a3=8-12=-4．
故选：D．
点评：本题考查了等差数列的性质，考查了等差中项的概念，是基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，在平行四边形ABCD中，E是BC的中点，G为AC与DE的交点，若下列式子中成立的是（ ）
A、log
| ||||
B、（
| ||||
C、（
| ||||
| D、log32＞log23 |
用数学归纳法证明不等式1+
+
+…+
＜n（n∈N*，且n＞1）时，不等式在n=k+1时的形式是（ ）
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
A、1+
| ||||||||||||
B、1+
| ||||||||||||
C、1+
| ||||||||||||
D、1+
|
设数列{an}是首项为1，公比为q（q≠-1）的等比数列，若{
}是等差数列，则（
+
）+（
+
）+…+（
+
）=（ ）
| 1 |
| an+an+1 |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| a3 |
| 1 |
| a4 |
| 1 |
| a2013 |
| 1 |
| a2014 |
| A、2012 | B、2013 |
| C、4024 | D、4026 |
为了得到函数y=sin（2x-
）的图象，只需把正弦曲线y=sinx上所有点（ ）
| π |
| 6 |
A、向右平移
| ||||
B、向左平移
| ||||
C、向右平移
| ||||
D、向左平移
|
过点（
，
）且被圆C：x2+y2-2x-4y=0截得的最短弦的弦长为（ ）
| 5 |
| 2 |
| 3 |
| 2 |
A、3
| ||
B、
| ||
C、
| ||
D、
|
若a，b∈R，且ab＞0，则下列不等式中，恒成立的是（ ）
| A、a2+b2＞2ab | ||
B、a+b≥2
| ||
C、a+b＞2
| ||
| D、a2+b2≥2ab |
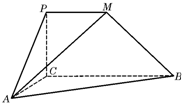如图，PCBM是直角梯形，∠PCB=90°，PM∥BC，PM=1，BC=2，又AC=1，∠ACB=120°，AB⊥PC，直线AM与直线PC所成的角为60°．