题目内容
设函数f(x)=2x3+tx2+x,g(x)=x2+tx+t+3,其中t∈R.已知函数g(x)有两个零点x1,x2,且0≤x1<1时,实数t的取值集合记为M.
(Ⅰ)求集合M;
(Ⅱ)f(x1)+f(x2)的取值范围.
(Ⅰ)求集合M;
(Ⅱ)f(x1)+f(x2)的取值范围.
考点:函数零点的判定定理
专题:函数的性质及应用
分析:(Ⅰ)问题转化为方程x2+tx+t+3=0有2个根,根据△>0,得到t的范围,从而求出集合M;
(Ⅱ)由韦达定理得:x1+x2=-t,x1•x2=t+3,从而f(x1)+f(x2)═-t3+4t2+11t,令h(t)=-t3+4t2+11t,(t<-2或t>6),求出h(t)的范围,从而得到答案.
(Ⅱ)由韦达定理得:x1+x2=-t,x1•x2=t+3,从而f(x1)+f(x2)═-t3+4t2+11t,令h(t)=-t3+4t2+11t,(t<-2或t>6),求出h(t)的范围,从而得到答案.
解答:
解:(Ⅰ)由g(x)=x2+tx+t+3有2个零点,
即方程x2+tx+t+3=0有2个根,
∴△=t2-4(t+3)>0,解得:t<-2或t>6,
∴M={t|t<-2或t>6};
(Ⅱ)由韦达定理得:x1+x2=-t,x1•x2=t+3,
∴f(x1)+f(x2)
=(2x13+tx12+x1)+(2x23+tx22+x2)
=2(x1+x2)[(x1+x2)2-3x1x2]+t(x1+x2)2-2tx1 x2+(x1+x2)
把x1+x2=-t,x1•x2=t+3,代入上式得:
f(x1)+f(x2)
=-2t[t2-3(t+3)]+t•t2-2(t+3)-t
=-t3+4t2+11t,
令h(t)=-t3+4t2+11t,(t<-2或t>6),
∴h′(t)=-3t2+8t+11=-(3t-11)(t+1),
当t<-2时,h′(t)<0,当t>6时,h′(t)<0,
∴h(t)在(-∞,-2)递减,在(6,+∞)递减,
而h(-2)=2,h(6)=-6,
∴h(t)>2或h(t)<-6,
∴f(x1)+f(x2)的取值范围是{h(t)|h(t)<-6或h(t)>2}.
即方程x2+tx+t+3=0有2个根,
∴△=t2-4(t+3)>0,解得:t<-2或t>6,
∴M={t|t<-2或t>6};
(Ⅱ)由韦达定理得:x1+x2=-t,x1•x2=t+3,
∴f(x1)+f(x2)
=(2x13+tx12+x1)+(2x23+tx22+x2)
=2(x1+x2)[(x1+x2)2-3x1x2]+t(x1+x2)2-2tx1 x2+(x1+x2)
把x1+x2=-t,x1•x2=t+3,代入上式得:
f(x1)+f(x2)
=-2t[t2-3(t+3)]+t•t2-2(t+3)-t
=-t3+4t2+11t,
令h(t)=-t3+4t2+11t,(t<-2或t>6),
∴h′(t)=-3t2+8t+11=-(3t-11)(t+1),
当t<-2时,h′(t)<0,当t>6时,h′(t)<0,
∴h(t)在(-∞,-2)递减,在(6,+∞)递减,
而h(-2)=2,h(6)=-6,
∴h(t)>2或h(t)<-6,
∴f(x1)+f(x2)的取值范围是{h(t)|h(t)<-6或h(t)>2}.
点评:本题考查了函数的零点问题,韦达定理,转化思想,考查了函数的单调性问题,是一道中档题.

练习册系列答案
相关题目
 如图所示,已知三棱锥P-ABC中,∠ACB=90°,BC=4,AB=20,D为AB的中点,且△PDB是等边三角形,PA⊥PC.
如图所示,已知三棱锥P-ABC中,∠ACB=90°,BC=4,AB=20,D为AB的中点,且△PDB是等边三角形,PA⊥PC.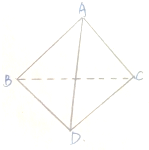 如图,三棱锥A-BCD中,DC⊥BC,BC=2
如图,三棱锥A-BCD中,DC⊥BC,BC=2