题目内容

求值：sin63°sin123°+cos117°sin33°．
考点：两角和与差的正弦函数
专题：三角函数的求值
分析：直接利用诱导公式化简，然后利用两角和与差的三角函数化简求解即可．
解答： 解：sin63°sin123°+cos117°sin33°
=sin63°cos33°-cos63°sin33°
=sin（63°-33°）
=sin30°
=
1
2
．
点评：本题考查两角和与差的三角函数，诱导公式的应用，基本知识的考查．
练习册系列答案
相关题目
在△ABC中，a-bcosC-ccosB的值为
 
．
直线y=kx+3与圆（x-2）2+（y-3）2=4相交于M、N两点，若|MN|≥2
3
，则直线倾斜角的取值范围是（　　）
A、[
π
6
，
5π
6
]
B、[0，
π
3
]∪[
2π
3
，π)
C、[0，
π
6
]∪[
5π
6
，π)
D、[
π
3
，
2π
3
]
设函数y=ln（cosx），x∈（-
π
2
，
π
2
）的图象是（　　）
A、
B、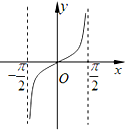
C、
D、
若集合S={y|y=-x2+2x，x∈R}，T={x∈R|y=
1-x2
}，则S∩T是（　　）
A、ϕB、TC、SD、有限集
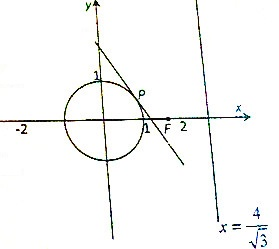已知动点M到点F（
3
，0）的距离与到直线x=
4
3
的距离之比为定值
3
2
，记M的轨迹为C．
（1）求C的方程，并画出C的简图；
（2）点P是圆x2+y2=1上第一象限内的任意一点，过P作圆的切线交轨迹C于R，Q两点．
（i）证明：|PQ|+|FQ|=2；
（ii）求RQ的最大值．
求证：当0＜x＜
π
2
时，sinx＜x＜tanx．
设函数f（x）=2x3+tx2+x，g（x）=x2+tx+t+3，其中t∈R．已知函数g（x）有两个零点x1，x2，且0≤x1＜1时，实数t的取值集合记为M．
（Ⅰ）求集合M；
（Ⅱ）f（x1）+f（x2）的取值范围．
如图，四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AB=1，AD=
3
，点F是PB的中点，点E在边BC上移动．
（1）求三棱锥E-PAD的体积；
（2）证明：无论点E在边BC的何处，都有PE⊥AF．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网