题目内容
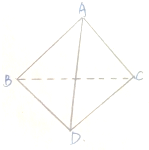如图，三棱锥A-BCD中，DC⊥BC，BC=2| 3 |
| 2 |
考点：直线与平面垂直的性质
专题：证明题,空间位置关系与距离
分析：先证明DC⊥AC，由DC⊥BC，BC∩AC=C，可证DC⊥平面ABC，从而可证AB⊥CD．
解答：
证明：∵CD=AC=2，AD=2
，
∴在△ACD中，有CD2+CA2=4+4=8=(2
2=AD2，
∴DC⊥AC，
又∵DC⊥BC，BC∩AC=C，
∴DC⊥平面ABC，
∵AB?平面ABC，
∴AB⊥CD．
| 2 |
∴在△ACD中，有CD2+CA2=4+4=8=(2
| 2) |
∴DC⊥AC，
又∵DC⊥BC，BC∩AC=C，
∴DC⊥平面ABC，
∵AB?平面ABC，
∴AB⊥CD．
点评：本题主要考查了直线与平面垂直的性质，属于基本知识的考查．
练习册系列答案
相关题目
如图，四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PA=AB=1，AD=
