题目内容
下列函数中值域是（0，+∞）的是（ ）
| A、y=log2（x2-2x-3） | ||
| B、y=x2+x+2 | ||
C、y=
| ||
| D、y=22x+1 |
考点：复合函数的单调性
专题：函数的性质及应用
分析：利用二次函数、对数函数、指数函数、反比例函数的性质，求得各个选项中函数的值域，从而得出结论．
解答：
解：∵函数y=log2（x2-2x-3）=log2[（x-1）2-4]的值域为R，不满足条件，故排除A．
∵y=x2+x+2=(x+
)2+
≥
，不满足值域是（0，+∞），故排除B．
∵函数y=
的值域为（0，+∞），故满足条件．
∵y=22x+1＞1，不满足值域是（0，+∞），故排除D，
故选：C．
∵y=x2+x+2=(x+
| 1 |
| 2 |
| 7 |
| 4 |
| 7 |
| 4 |
∵函数y=
| 1 |
| |x| |
∵y=22x+1＞1，不满足值域是（0，+∞），故排除D，
故选：C．
点评：本题主要考查复合函数的单调性，二次函数、对数函数的性质，体现了转化的数学思想，属于基础题．
练习册系列答案
相关题目
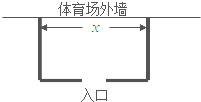备受瞩目的巴西世界杯正在如火如荼的进行，为确保总决赛的顺利进行，组委会决定在位于里约热内卢的马拉卡纳体育场外临时围建一个矩形观众候场区，总面积为72m2（如图所示）．要求矩形场地的一面利用体育场的外墙，其余三面用铁栏杆围，并且要在体育馆外墙对面留一个长度为2m的入口．现已知铁栏杆的租用费用为100元/m．设该矩形区域的长为x（单位：m），租用铁栏杆的总费用为y（单位：元）
如图是计算y=f（x）函数值的程序框图．