题目内容
计算或花间下列各式:
(1)2log510+log50.25
(2)(2a
b
)(-6a
b
)÷(-3a
b
)(a>0,b>0).
(1)2log510+log50.25
(2)(2a
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 6 |
| 5 |
| 6 |
考点:对数的运算性质
专题:函数的性质及应用
分析:(1)直接利用对数的运算法则化简求值即可.
(2)直接利用有理指数幂的运算法则求解即可.
(2)直接利用有理指数幂的运算法则求解即可.
解答:
解:(1)原式=log5102+log50.25=log5(102×0.25)=log525=2;
(2)原式=(-12a
b
)÷(-3a
b
)=4a.
(2)原式=(-12a
| 7 |
| 6 |
| 5 |
| 6 |
| 1 |
| 6 |
| 5 |
| 6 |
点评:本题考查指数与对数的运算法则的应用,基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设奇函数f(x)在(0,+∞)上为增函数,且f(2)=0,则不等式
<0的解集为( )
| f(x)-f(-x) |
| x |
| A、{x|-2<x<0或0<x<2} |
| B、{x|x<-2或0<x<2} |
| C、{x|x<-2或x>2} |
| D、{x|-2<x<0或x>2} |
若y=f(x)在x>0上可导,且满足:xf′(x)-f(x)>0恒成立,又常数a,b满足a>b>0,则下列不等式一定成立的是( )
| A、bf(a)>af(b) |
| B、af(a)>bf(b) |
| C、bf(a)<af(b) |
| D、af(a)<bf(b) |
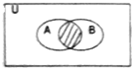 已知全集U=R,集合A={y|y=sinx,x∈R}和B={x|x2-x<0}的关系的韦恩图(vean)如图所示,则阴影部分表示的集合是( )
已知全集U=R,集合A={y|y=sinx,x∈R}和B={x|x2-x<0}的关系的韦恩图(vean)如图所示,则阴影部分表示的集合是( )| A、{x|-1≤x<1} |
| B、{x|-1<x<1} |
| C、{x|0<x<1} |
| D、{x|0<x≤1} |
下列函数中值域是(0,+∞)的是( )
| A、y=log2(x2-2x-3) | ||
| B、y=x2+x+2 | ||
C、y=
| ||
| D、y=22x+1 |