题目内容
8.在△ABC中,AB=AC,D为线段AC的中点,若BD的长为定值l,则△ABC面积的最大值为$\frac{2}{3}$$\sqrt{l}$(用l表示).分析 先在△ABD中利用余弦定理表示出cosA,进而求得sinA的表达式,进而代入三角形面积公式利用转化为二次函数来解决.
解答 解:cosA=$\frac{{b}^{2}+\frac{{b}^{2}}{4}{-l}^{2}}{2b•\frac{1}{2}b}$=$\frac{5}{4}$-${(\frac{l}{b})}^{2}$,
∴S△ABC=$\frac{1}{2}$b2$\sqrt{1{-(\frac{5}{4}{-(\frac{l}{b})}^{2})}^{2}}$=$\frac{1}{8}$$\sqrt{-{9{(b}^{2}-\frac{20}{9}l)}^{2}+\frac{256}{9}l}$≤$\frac{2}{3}$$\sqrt{l}$,
故答案为:$\frac{2}{3}$$\sqrt{l}$.
点评 本题主要考查了余弦定理和正弦定理的运用.解题过程中充分利用好等腰三角形这个条件,把表达式的未知量减到最少.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.已知函数f(x)=kx-1,其中实数k随机选自区间[-1,2].则对任意的x∈[-1,1],f(x)≤0的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
3. 在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如下面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )
在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如下面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )
 在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如下面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )
在一段时间内有2000辆车通过高速公路上的某处,现随机抽取其中的200辆进行车速统计,统计结果如下面的频率分布直方图所示.若该处高速公路规定正常行驶速度为90km/h~120km/h,试估计2000辆车中,在这段时间内以正常速度通过该处的汽车约有( )| A. | 30辆 | B. | 300辆 | C. | 170辆 | D. | 1700辆 |
13.设Sn为等差数列{an}的前n项和,若已知S6<S7,S7>S8,则下列叙述中正确的个数有( )
①S7是所有Sn(n∈N*)中的最大值;
②a7是所有an(n∈N*)中的最大值;
③公差d一定小于0;
④S9一定小于S6.
①S7是所有Sn(n∈N*)中的最大值;
②a7是所有an(n∈N*)中的最大值;
③公差d一定小于0;
④S9一定小于S6.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
18.已知函数f(x)=|lgx|,若0<a<b,且f(a)=f(b),则a+4b的取值范围是( )
| A. | (4,+∞) | B. | [4,+∞) | C. | (5,+∞) | D. | [5,+∞) |
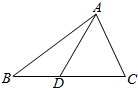 如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.
如图,在△ABC中,AB=12,$AC=3\sqrt{6}$,$BC=5\sqrt{6}$,点D在边BC上,且∠ADC=60°.