题目内容
C
+C
+C
+…+C
= .已知A
=56C
,则n= .
2 2 |
2 3 |
2 4 |
2 10 |
5 n |
7 n |
考点:组合及组合数公式
专题:排列组合
分析:利用组合数公式的性质Cn+13-cn3=Cn2,可得 C22+C32+C42+…+
=C33 +(C43-C33)+(C53-C43)+…+(C113-C103),化简得到结果;
直接展开排列数公式和组合数公式化简求解n的值.
| C | 2 10 |
直接展开排列数公式和组合数公式化简求解n的值.
解答:
解:∵Cn+13-cn3=Cn2,
∴C
+C
+C
+…+C
=C33 +(C43-C33)+(C53-C43)+…+(C113-C103)=C113 ;
由A
=56C
,得
=56
,即(n-5)(n-6)=90,解得:n=15或n=-4(舍).
故答案为:
,15.
∴C
2 2 |
2 3 |
2 4 |
2 10 |
由A
5 n |
7 n |
| n! |
| (n-5)! |
| n! |
| 7!•(n-7)! |
故答案为:
| C | 3 11 |
点评:本题主要考查组合数公式的性质应用,利用了组合数公式的性质Cn+13-cn3=Cn2,即Cn2 +cn3 =Cn+13,属于基础题.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
 如图,在棱长为1的正方体ABCD-A1B1C1D1中.
如图,在棱长为1的正方体ABCD-A1B1C1D1中.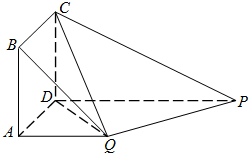 在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ=
在如图所示的多面体中,四边形ABCD为正方形,四边形ADPQ是直角梯形,AD⊥DP,CD⊥平面ADPQ,AB=AQ= 如图,在矩形OABC中,点E,F分别在AB,BC上,且满足AB=3AE,BC=3CF,若
如图,在矩形OABC中,点E,F分别在AB,BC上,且满足AB=3AE,BC=3CF,若